PHYS 170

Lecture 12 - Oscillatory Motion

Introduction

Simulation - Spring Oscillations with Damping (click to hide)

Canvas not supported
Drag the object to change the amplitude.
The slider for damping adjusts the value of \(\frac{\gamma}{2 \omega}\) and defaults to 0 (no damping).
When the slider value is set to 1, the system is critically damped. A value greater than or less than 1 represents the cases of over-damping and under-damping respectively. Observe the difference among the three different cases of damping.
The calculations below is updated the moment the simulation is paused.
Calculations will appear here.

Oscillations in physics is described by the equation:

$$ \ddot{x} = -\omega^2 x $$
$\ddot{x} = \frac{d^2 x}{dt^2}$ is the Newtonian notation for the second time derivative and $\omega$ is called the "angular frequency". Roughly speaking, $\omega$ represents how rapidly the system is oscillating.

This equation is also known as the SHO equation, where "SHO" stands for "simple harmonic oscillation". It is the oscillation caused by a simple restoring force (such as that of a spring obeying Hooke's Law) in the absence of friction and other external forces. It is a very important equation in physics. Even when a system is not strictly simple harmonic, often it could still be described by this equation to a good approximation.

A typical oscillator we will return to often is the spring-mass system on the left. In the absence of friction, the angular frequency of this system is given by:
$$ \omega_{\text{spring}} = \sqrt{\frac{k}{m}} $$
where $k$ is the spring constant first introduced in Chapter 7.
Another common oscillator we will look is the simple pendulum (see Chapter 7). The angular frequency of this system is given by:
$$ \omega_{\text{pendulum}} = \sqrt{\frac{g}{l}} $$

Simulation - Hooke's Law (click to hide)

Canvas not supported
Drag on the mass to change its position. Click "Play" to start the oscillation.

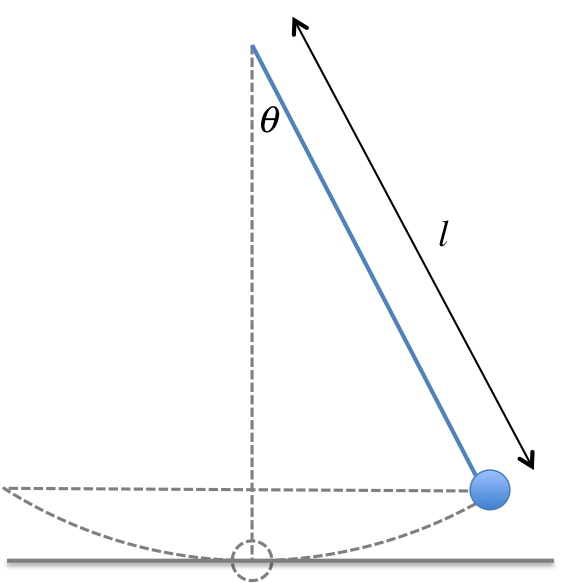
Simulation - Simple Pendulum (click to hide)

Canvas not supported

Drag on the ball to change the length.
Drag on the bar to change the angle.
Click on the clock to reset the timer.
The mass of the object is fixed to be \(m = 1kg\).
The grey horizontal line represents the lowest level of the pendulum trajectory, used as a reference level for height measurement.

Activity

Use the clock to time 10 oscillations and deduce the period. Repeat for a different length and see how the period changes.

Other Variables

In Chapter 10a on rotational motion, we called $\omega$ the "angular velocity", but in the context of oscillation this variable is usually called the "angular frequency". Other than the difference in name, it turns out $\omega$ obeys exactly the same relationship with other variables that are used to describe oscillations:

Name Symbol Unit Meaning
Angular frequency \(\omega\) \( rad/s\) rate of oscillation
Period \(T\) \(s\) time to complete one oscillation
Frequency \(f\) \(Hz\) number of oscillations per second

Here are the equations that connect the variables together:

$$ \begin{eqnarray} \omega &=& \frac{2\pi}{T} &=& 2\pi f \end{eqnarray} $$

Try It Yourself (click to show)

Question will be loaded by load_exercise_example_all() defined in script_question.js
Question will be loaded by load_exercise_example_all() defined in script_question.js
Question will be loaded by load_exercise_example_all() defined in script_question.js

Try It Yourself (click to show)

Question will be loaded by load_exercise_example_all() defined in script_question.js
Question will be loaded by load_exercise_example_all() defined in script_question.js

Solution to the SHO Equation

The general solution of the oscillation equation is:

$$ x = A \cos(\omega t + \phi) $$

Name Symbol Unit Meaning
Amplitude \(A\) \(m\), or other units maximum displacement, or other meanings (such as angle) depending on the system
Phase constant \(\phi\) \(rad\) shift of the $\cos$ function along the $t$ axis

Simulation - Graph of Simple Harmonic Oscillation (click to hide)

Canvas not supported
Graph of Simple Harmonic Oscillation
General solution to $\ddot{y} = - \omega^2 y$:
Calculations will appear here.

Math Review - Differentiation of Trignometric Functions

You need to know how to differentiate $\cos$ and $\sin$ functions to proceed further. We will start with two basic facts: $$ \begin{eqnarray} \frac{d}{d\theta}\sin\theta &=& \cos \theta \\ \frac{d}{d\theta}\cos\theta &=& -\sin \theta \end{eqnarray} $$

In physics we often differentiate with respect to $t$, like so: $$ \begin{eqnarray} \frac{d}{dt}\sin\omega t &=& \omega \cos \omega t \\ \frac{d}{dt}\cos\omega t &=& -\omega \sin \omega t \end{eqnarray} $$ Note that every time derivative "pulls down" a factor of $\omega$ due to the chain rule of calculus.

The last step is to include the phase constant $\phi$. Fortunately, $\phi$ just comes along for the ride and do not change the results: $$ \begin{eqnarray} \frac{d}{dt}\sin(\omega t + \phi) &=& \omega \cos (\omega t + \phi) \\ \frac{d}{dt}\cos(\omega t + \phi) &=& -\omega \sin (\omega t + \phi) \end{eqnarray} $$ Note that every time derivative "pulls down" a factor of $\omega$ due to the chain rule of calculus.

Question will be loaded by load_exercise_example_all() defined in script_question.js
Question will be loaded by load_exercise_example_all() defined in script_question.js

Notations

Name Symbol Unit Meaning
Angular frequency \(\omega\) \( rad/s\) rate of oscillation
Period \(T\) \(s\) time to complete one oscillation
Frequency \(f\) \(Hz\) number of oscillation per second
Amplitude \(A\) \(m\), or other units maximum displacement, or other meanings (such as angle) depending on the system
Phase constant \(\phi\) \(rad\) shift of the $\cos$ function along the $t$ axis