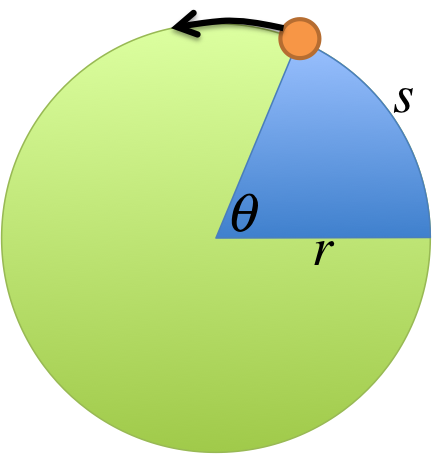
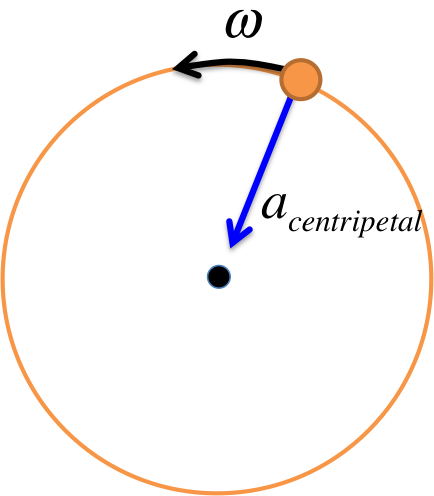
For the rest of the semester, you will need to familiarize yourself with the following variables, which will form the basic vocabulary for the topics to follow.
| Name |
Symbol |
Unit |
Meaning |
| Angular velocity |
\(\omega\) |
\( rad/s\) |
rate of change of angle |
| Linear (or tangential) speed |
\(v\) |
\( m/s \) |
distance traveled per second |
| Period |
\(T\) |
\(s\) |
time to complete one cycle |
| Frequency |
\(f\) |
\(Hz = rps\) |
number of cycles per second |
\(rps\) stands for "revolutions per second", which is identical to \(Hz\) and \(s^{-1}\).
Here are the equations that connect the variables together:
$$
\begin{eqnarray}
v &=& \omega r\\
\omega &=& \frac{2\pi}{T} &=& 2\pi f
\end{eqnarray}
$$
You already proved \(\omega = \frac{2\pi}{T}\) earlier in the exercise "angular velocity 3", from this we can show the other equations. We will begin with \(v\). In one period \(T\), the distance traveled should just be the circumference of the circle, i.e. \(2\pi r\). Therefore \(v\), "distance traveled per second", is given by:
$$
\begin{eqnarray}
v &=& \frac{2\pi r}{T} = \frac{2\pi }{T}r\\
&=& \omega r
\end{eqnarray}
$$
As for the equation relating \(f\), you could ask the following question: suppose it takes an object \(T=1/2s\) to complete one cycle, how many revolution can it make per second? The answer is 2, so \(f=\frac{1}{T}\). If it takes \(T=1/3s\) for one revolution, how many revolutions can it make per second? Some thinking tells you it would be 3, again giving \(f=\frac{1}{T}\). Since we already know \(\omega = \frac{2\pi}{T}\), we have:
$$
\begin{eqnarray}
\omega &=& \frac{2\pi}{T} = 2\pi\frac{1}{T}\\
&=& 2\pi f
\end{eqnarray}
$$
Try It Yourself (click to show)
If it can go around twice in \(40s\), then it takes \(20s\) to go around once, therefore the period \(T\) is \(20s\).
$$
\begin{eqnarray}
\omega &=& \frac{2\pi}{T} = 0.31 rad/s\\
f &=& \frac{1}{T} = 0.05Hz \\
v &=& \omega r = 0.62m/s
\end{eqnarray}
$$
The question tells you \(v=0.5m/s\), from this you can find everything else.
$$
\begin{eqnarray}
\omega &=& \frac{v}{r} = 0.25 rad/s\\
T &=& \frac{2\pi}{\omega} = 25.13 s \\
f &=& \frac{1}{T} = 0.04Hz
\end{eqnarray}
$$
The question tells you \(v=0.5m/s\), from this you can find everything else.
$$
\begin{eqnarray}
f &=& 120rpm = \frac{120 rev}{1 min} \\
&=& \frac{120 rev}{60s} = \frac{2 rev}{1s} \\
&=& 2rps = 2Hz \\
\omega &=& 2\pi f = 12.57rad/s \\
T &=& \frac{1}{f} = 0.5 s \\
v &=& \omega r = 25.13 m/s
\end{eqnarray}
$$
The earth takes 1 day to spin around once, so we know the period is \(T=1day = 86400s\).
$$
\begin{eqnarray}
\omega &=& \frac{2\pi}{T} = 72.72\times 10^{-6}rad/s \\
f &=& \frac{1}{T} = 11.57\times 10^{-6} Hz \\
v &=& \omega r = (72.72\times 10^{-6})(6.37\times 10^6) = 463.23m/s
\end{eqnarray}
$$