PHYS 170

Gravity is one of the four fundamental forces of nature known to mankind, but it is also one of the most mysterious. Physicists are still trying to find a complete theory of quantum gravity, which is likely a big missing piece in our understanding of our universe and space-time. In this course, we will not worry ourselves with the incredibly difficult and subtle behaviors of gravity in modern physics but will instead focus on "Newtonian gravity", they theory that was pioneered by Newton a few hundred years ago.

Because we will often compute the gravitational interaction with stars and planets, it is useful to keep the following information handy. There is no need to memorize the numbers though, as they will be provided to you in the exam.

Distance between the Earth and the Moon: $R_{EM} = 3.85\times 10^{8}m$
Distance between the Earth and the Sun: $R_{ES} = 1.5\times 10^{11}m$

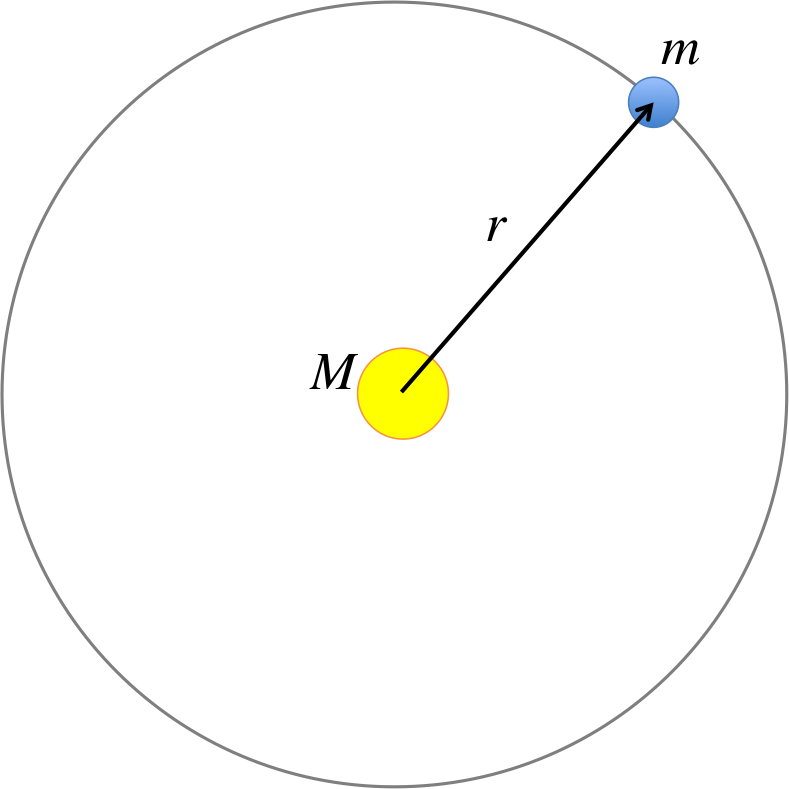
Two masses separated by distance $r$ will experience a mutually attractive gravitational force. The magnitude of the force is given by:

$$ \begin{eqnarray} F &=& G \frac{m_1 m_2}{r^2} \end{eqnarray} $$

where $G=6.67\times 10^{-11}Nm^2kg^{-2}$

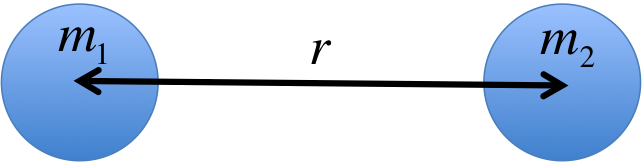
$G$ is called the gravitational constant, which is not to be confused with $g=9.8m/s^2$ (the acceleration due to gravity on the surface of the Earth). A key observation is how incredibly small $G$ is (in SI unit). The smallness of this number is the reason why gravity is considered the weakest force out of the four fundamental forces of nature. The gravitational interaction between two objects of "everyday scale" is quite negligible, as you could see in the example below.

Try It Yourself (click to show)

The last example confirms the equivalence of $mg$ and $F=G\frac{m M}{R^2}$ (omitting the subscript "$E$"). This equivalence gives a useful formula for $g$: $$ \begin{eqnarray} mg &=& G\frac{m M}{R^2}\\ \Rightarrow g &=& G\frac{M}{R^2} \end{eqnarray} $$ In other words, the acceleration due to gravity on the surface of a planet can be computed using the mass and the radius of the planet.

Try It Yourself (click to show)

Orbtal motion is governed by gravitational force and centripetal force: $$ \begin{eqnarray} F_g &=& G\frac{Mm}{r^2} \\ F_{cent} &=& m r \omega^2 \end{eqnarray} $$ To put it simply, gravity provides the centripetal force necessary to keep the mass $m$ in orbit around $M$. Therefore, we have $F_{cent} = F_g$:

$$ \begin{eqnarray} G\frac{Mm}{r^2} &=& m r \omega^2 \end{eqnarray} $$

Try It Yourself (click to show)

The gravitational potential energy of two masses separated by distance $r$ is given by:

At this point you may wonder about another equation for gravitational potential energy you learned in Chapter 7, namely: $$ PE = mgh $$ Without going into the mathematical details, $PE = mgh$ is actually a special case of $PE = -G \frac{M m}{r}$. $PE = mgh$ assumes uniform gravitational field (i.e. $g$ is a constant), which is valid as long as you stay on the surface of the planet. If you travel far above a planet (to the extent that $g$ weakens and can no longer be treated as a constant), then you must use $PE = -G \frac{M m}{r}$ instead. You will see this in the "launching problems" below.

Conservation of energy can be applied just as Chapter 7: $$ \begin{eqnarray} KE_1 + PE_1 &=& KE_2 + PE_2 \\ \Rightarrow \frac{1}{2}mv_1^2 - G \frac{M m}{r_1} &=& \frac{1}{2}mv_2^2 - G \frac{M m}{r_2} \end{eqnarray} $$ Note that $m$ could be eliminated from both sides.

Try It Yourself (click to show)