Lecture 05 - Applications of Newton's Laws

Friction

Simulation - friction (click to hide)

Drag on the surface of the incline to change the angle.
The force diagram can also be dragged to a different location.
The applied force can be adjusted by the slider. Click the "Play" button to see the motion.
We assume $\mu_s = \mu_k $ (static and kinetic coefficients of friction) for simplicity.

There are two types of friction:

static friction
kinetic friction

Kinetic friction will be our main focus in this course.

static friction

Static friction is used when an object is at rest. For example, if you apply a force to push a big heavy box on a rough floor yet it refuses to move, it is due to the static friction between the box and the floor acting against your applied force. Static friction obeys the following equation: $$ \begin{eqnarray} f_{s, max}&=& \mu_s F_n \end{eqnarray} $$ $\mu_s$ is a dimensionless (no unit) number called the coefficient of static friction, and $F_n$ is the normal force. $f_{s, max}$ is the maximum possible value of static friction achievable. Approximately speaking, $\mu_s$ describes how rough the contact surfaces are between the box and the floor. The rougher the surfaces, the larger is $\mu_s$, and the higher the value of $f_{s, max}$.

An equivalent way to express the relationship above is: $$ \begin{eqnarray} f_s &\leq& \mu_s F_n \end{eqnarray} $$

One can see from the simulation above that the static friction is not a fixed number, instead it changes depending on the external force. That is why the relation obeyted by $f_s$ is not a simple equation but an inequality.

kinetic friction

Kinetic friction is used when an object is in motion. For example, if you apply a force to push a big heavy box on a rough floor, once it is in motion, the friction coming from the floor is called kinetic friction. Different from static friction, we can describe kinetic friction by a simple equation (as opposed to an inequality):

$$ \begin{eqnarray} f_k &=& \mu_k F_n \end{eqnarray} $$

$\mu_k$ is a dimensionless (no unit) number called the coefficient of kinetic friction, and $F_n$ is the normal force. Once again, the rougher the surfaces, the larger is $\mu_k$, and the higher the value of $f_k$.

In this course we will mostly be dealing with kinetic friction (and rarely with static friction), so for simplicity we will often omit the subscript "$s$" and simply write the equation above as $f=\mu F_n$.

Question will be loaded by load_exercise_example_all() defined in script_question.js

Try It Yourself (click to show)

Question will be loaded by load_exercise_example_all() defined in script_question.js

Centripetal Force and Acceleration

Simulation - The Basics of Rotational Motion (click to hide)

Adjust the sliders to see:

how long it takes for the object to go around the circle once (period);
how many revolutions the object can complete in one second (frequency);
how many radians the object can cover per second (angular velocity).

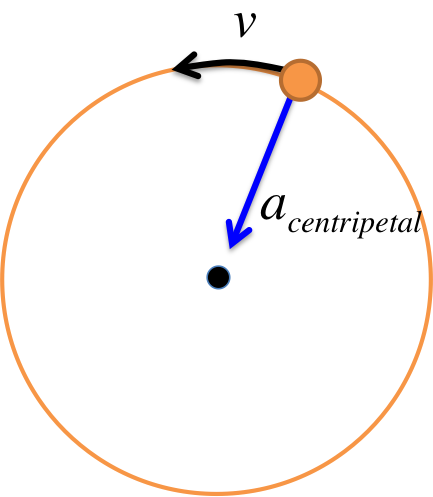
The object on the left is undergoing uniform circular motion, meaning its speed stays the same as it goes around. Here comes the unusual statement:

During uniform circular motion, there is an acceleration on the object pointing toward the center given by:

$$ a_{\text{centripetal}} = \frac{v^2}{r} $$

This acceleration is called the "centripetal acceleration".

The above equation can be rewritten in terms of the "angular velocity" $\omega$ using the fact that $v = \omega r$: $$ a_{\text{centripetal}} = \frac{(\omega r)^2}{r} = r \omega^2$$ Angular velocity will be discussed in great details in Chapter 10a.

Why should there be an acceleration if the object is not speeding up nor slowing down? This is again related to the difference between velocity and speed as explained here in chapter 2. During uniform circular motion, the speed (i.e. the magnitude of the velocity) stays constant but the velocity does not. The velocity points in different direction as the object goes around the circle, even though its magnitude never changes. Since acceleration is the rate of change of velocity (not the speed), you get a non-zero acceleration. In other words, the centripetal acceleration describes the change in the direction of the velocity.

Newton's Second Law ($F=ma$) tells us any acceleration implies the presence of a net force. In this case, the centripetal acceleration must be caused by a force pointing toward the center, called the "centripetal force", given by:

$$F_{\text{centripetal}} = m a_{\text{centripetal}} = \frac{mv^2}{r} = m r \omega^2 $$

The physical origin of the centripetal force is depends on the situation. For example, the centripetal force that keeps the moon in orbit around the earth is the force of gravity.

Later in the semester (starting with Chapter 10, but can be ignored for now), you will need to familiarize yourself with the following variables, which will form the basic vocabulary for the topics to follow.

Name	Symbol	Unit	Meaning
Angular velocity	$\omega$	$ rad/s$	rate of change of angle
Linear (or tangential) speed	$v$	$ m/s $	distance traveled per second
Period	$T$	$s$	time to complete one cycle
Frequency	$f$	$Hz = rps$	number of cycles per second

$rps$ stands for "revolutions per second", which is identical to $Hz$ and $s^{-1}$.

Here are the equations that connect the variables together:

$$ \begin{eqnarray} v &=& \omega r\\ \omega &=& \frac{2\pi}{T} &=& 2\pi f \end{eqnarray} $$

Simulation - Centripetal Force (click to hide)

Adjust the sliders to see how the trajectory is affected.
Can you calculate the radius of the trajectory?

Video - Centripetal Force (click to show)

Question will be loaded by load_exercise_example_all() defined in script_question.js

Try It Yourself (click to show)

Question will be loaded by load_exercise_example_all() defined in script_question.js

Notations

Name	Symbol	Unit	Meaning
Friction	$f$	$ N$	force against motion
Coefficient of friction	$\mu$	no unit	the roughness of the contact surfaces
Centripetal acceleration	$a_{cent}$	$m/s^2$	radially inward acceleration of an object undergoing uniform circular motion
Centripetal force	$F_{cent}$	$N$	radially inward force required to keep an object in uniform circular motion

PHYS 170

Introduction

Friction

Simulation - friction (click to hide)

static friction

kinetic friction

Try It Yourself (click to show)

Centripetal Force and Acceleration

Simulation - The Basics of Rotational Motion (click to hide)

Simulation - Centripetal Force (click to hide)

Video - Centripetal Force (click to show)

Try It Yourself (click to show)

Notations

Name	Symbol	Unit	Meaning
Angular velocity	\(\omega\)	\( rad/s\)	rate of change of angle
Linear (or tangential) speed	\(v\)	\( m/s \)	distance traveled per second
Period	\(T\)	\(s\)	time to complete one cycle
Frequency	\(f\)	\(Hz = rps\)	number of cycles per second

Name	Symbol	Unit	Meaning
Friction	\(f\)	\( N\)	force against motion
Coefficient of friction	\(\mu\)	no unit	the roughness of the contact surfaces
Centripetal acceleration	\(a_{cent}\)	\(m/s^2\)	radially inward acceleration of an object undergoing uniform circular motion
Centripetal force	\(F_{cent}\)	\(N\)	radially inward force required to keep an object in uniform circular motion