PHYS 170

Roughly speaking, a degree of freedom $f$ is a way a molecule can move. For example, a molecule that can move in $x, y, z$ directions has 3 translational degrees of freedom. Besides translation, there are other types of motion, such as rotation and vibration. Different types of molecules have different number of degrees of freedom.

Number of Degrees of Freedom

Molecule type	Translational	Rotational	Vibrational	Total, $f$
Monatomic	3	0	0	3
Diatomic (low $T$)	3	0	0	3
Diatomic (middle $T$)	3	2	0	5
Diatomic (high $T$)	3	2	2	7

For diatomic molecules at low temperature, some degrees of freedom gets "frozen" due to quantum effects. It is as if the molecules at lower temperature ceases to vibrate, and at even lower temperature they would stop rotating as well.

Internal Energy, $U$

The internal energy of a gas depends on the number of degrees of freedom of the molecules:

Combining the above equation with the ideal gas law $PV = nRT = NkT$, we get: $$ U = \frac{f}{2}PV = \frac{f}{2}nRT = \frac{f}{2}NkT $$ A key point to observe is that $U\propto T$, so if $T$ stays the same, the internal energy stays the same as well.

Change in Internal Energy, $\Delta U$

When the state of a gas changes, the change in internal energy is computed by:

Try It Yourself (click to show)

The term "work" in physics means energy transfer in general, in thermodynamics it generally refers to all energy transfer except heat $Q$. In this course, the only type of work we will study is work done by a gas as it expands or contracts slowly. In this case, work can be calculated using the following:

The symbol $W$ above means "work done by the gas", or $W_{by}$ if you want be explicit.

When $W>0$ the gas is spending (and therefore losing) energy. A similar variable you will often see is "work done on the gas", $W_{on}$. They are related by $W_{on} = -W_{by}$, in other words, they differ only by a negative sign. In this course, our $W$ is always $W_{by}$, so beware if you read different books their $W$ may mean $W_{on}$ and some equations will appear to have an additional negative signs as a result.

If you find the signs for $W$ confusing, then remember the following rules:

• $W\gt 0$ for gas expansion
• $W\lt 0$ for gas compression

Try It Yourself (click to show)

The First Law of Thermodynamics is commonly stated as follows:

Note that all three variables $\Delta U$, $Q$, and $W$ are measured in $J$ so be sure not to mix them up.

In essence, the first law conveys the idea of conservation of energy. For example, a gas that gains $100J$ of heat ($Q=+100J$) but does $70J$ of work ($W=70J$, i.e. spends $70J$ of energy expanding), then the net gain in energy is only $30J$ ($\Delta U = 100J - 70J = 30J$). Imagine you got paid $\$100$, but spend $\$70$, then your net gain is only $\$30$.

Try It Yourself (click to show)

While generally there are many ways to change the state a system, we often consider the following 4 special cases:

• Isobaric process - $P$ is fixed
• Isochoric (or isovolumetric) process - $V$ is fixed
• Isothermal process - $T$ is fixed
• Adiabatic process - $Q=0$, i.e. no heat exchange, thermally insulated

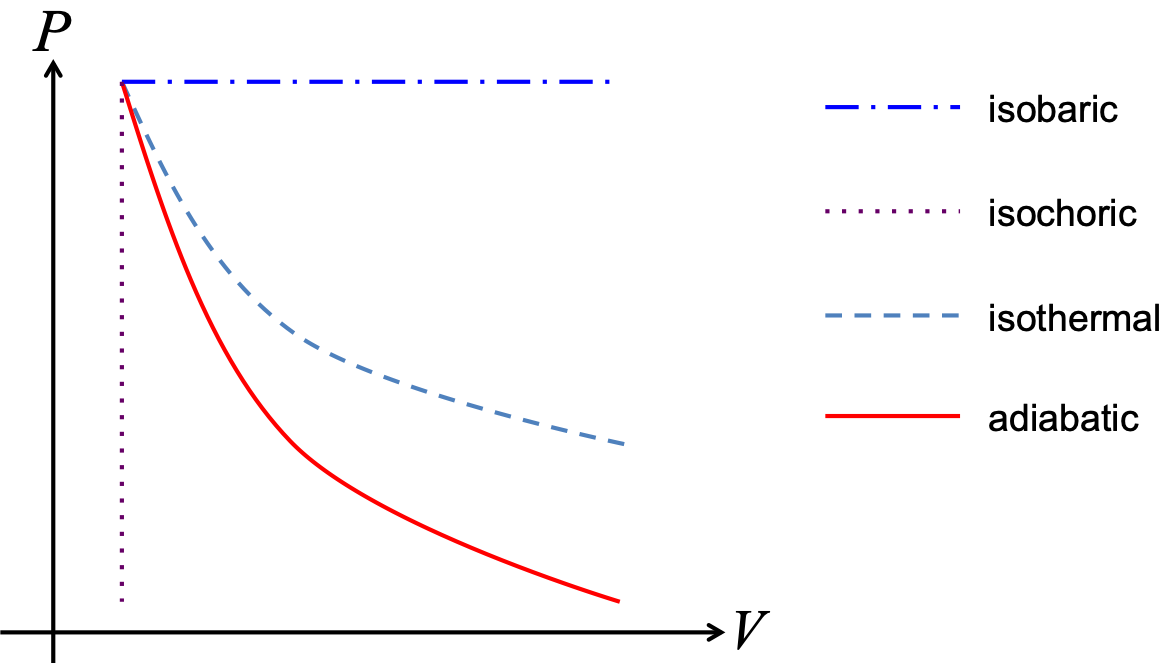
The isothermal curve is really just the ideal gas law $PV = nRT \Rightarrow P = \frac{nRT}{V}$, in other words $P\propto \frac{1}{V}$.

The adiabatic curve looks like an isothermal curve, except that it is slightly steeper. Mathematically, it is given by $P\propto \frac{1}{V^\gamma}$, where $\gamma = \frac{f+2}{f}$. The curve is also commonly written as $PV^\gamma = \text{constant}$.

Name	Symbol	Unit	Meaning
Degrees of freedom	$f$	no unit	number of ways a molecule can move
Internal energy	$U$	$ J $	energy of a thermodynamical system
Change in Internal energy	$\Delta U$	$ J $	$U_f - U_i$
Work done by the system	$W$	$J$	energy transfer through mechanical work by the system
Heat into the system	$Q$	$J$	energy transfer into the system due to temperature difference