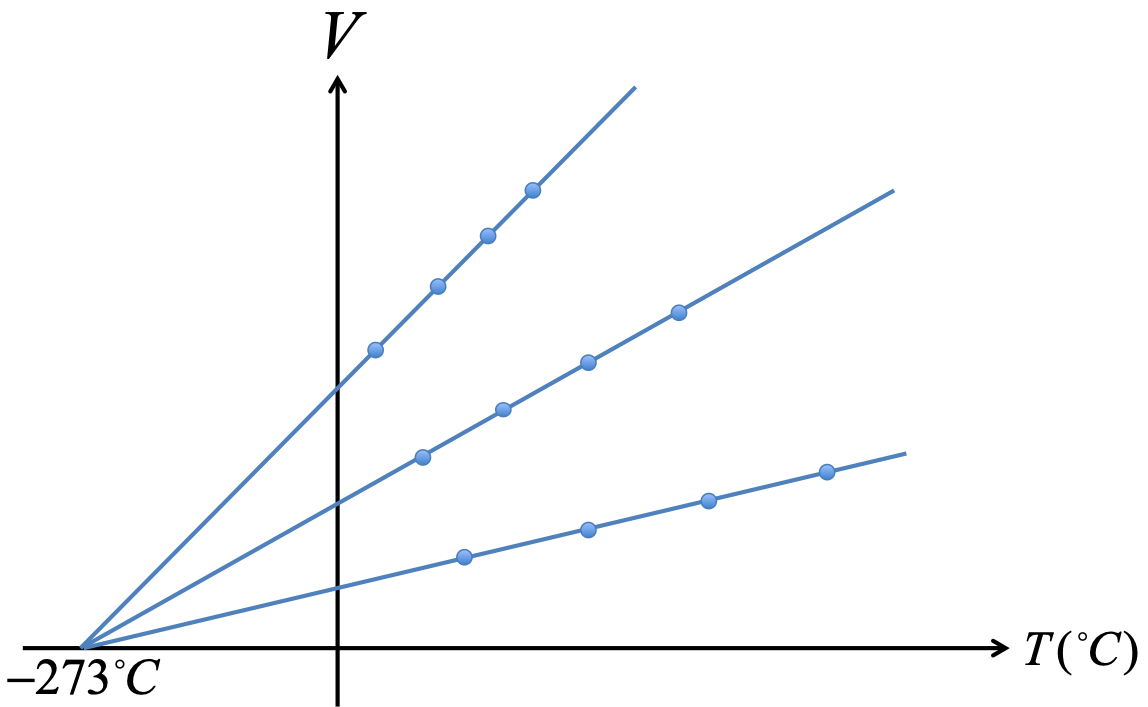
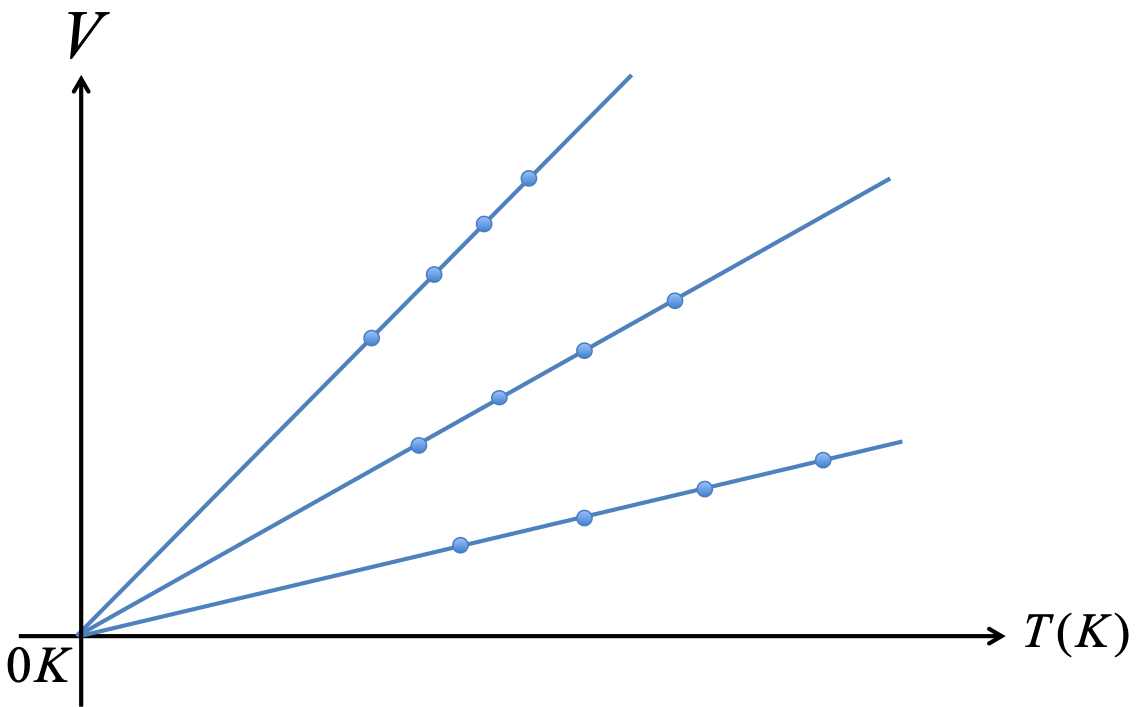
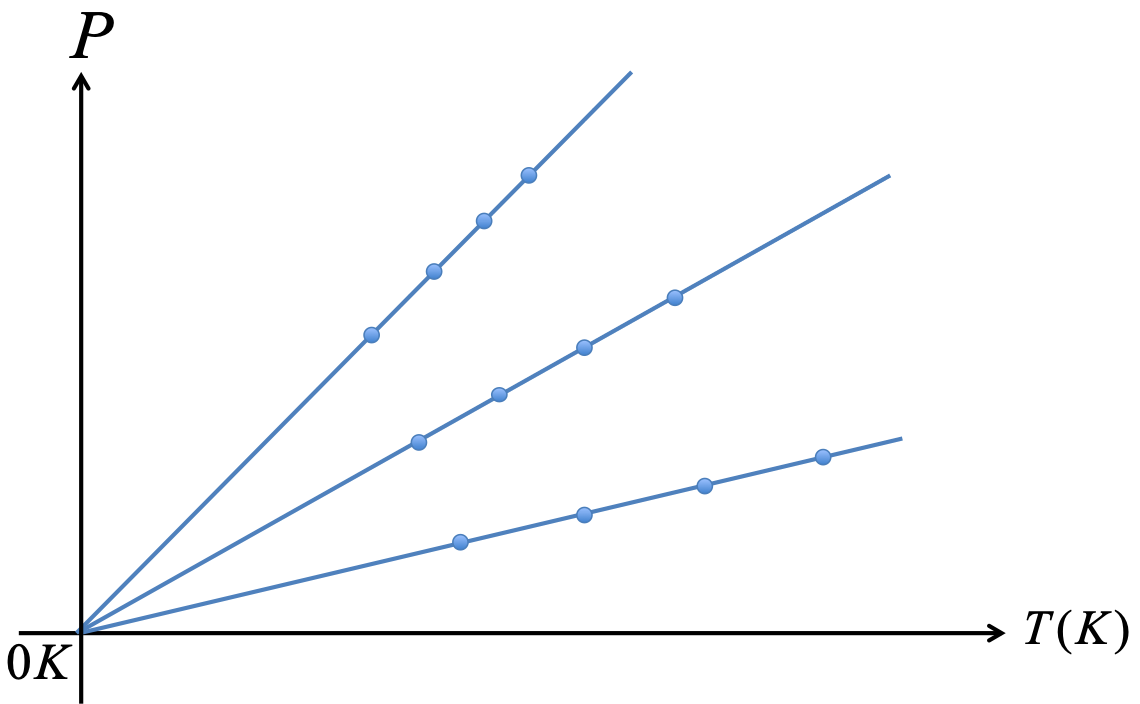
An ideal gas is a gas of point particles which has no other interactions besides collision among molecules. There is no intermolecular force. An ideal gas obeys the ideal gas law:
$$
PV = nRT
$$
where $R=8.31JK^{-1}mol^{-1}$ is the ideal gas constant, $n$ is the number of moles.
SI Unit
| $P$ |
$Pa$ |
| $V$ |
$m^3$ |
| $T$ |
$K$ |
| $n$ |
$mol$ |
Real gas molecules have non-zero volume (i.e. not point particles), and there is generally intermolecular force. However, for most gases at room temperature the size of the gas molecules are small compared to the whole volume of the gas, and the molecules are usually separated far enough for the intermolecular forces to be negligible (except when the gas is close to phase transition) so the ideal gas law usually works very well.
Review - Number of Moles $n$ Vs Number of molecules $N$
$n$ and $N$ are related to each other via $N= n N_A$, where $N_A = 6\times 10^{23}$ is the Avogadro's number. $N_A$ is the number of molecules in 1 mole of gas.
A good analogy to Avogadro's number is the concept of dozen used in a bakery. You can think of $N_A^{\text{baker}} = 12$ for a baker. So if you buy 3 dozens of donuts, it means you are buying $N = nN_A = (3)(12) = 36$ donuts.
Chemistry
| Number of moles, $n$ |
Number of molecules, $N = n N_A$ |
| $1$ |
$6\times 10^{23}$ |
| $2$ |
$12\times 10^{23}$ |
| $3$ |
$18\times 10^{23}$ |
| $4$ |
$24\times 10^{23}$ |
Bakery
| Number of dozens, $n$ |
Number of donuts, $N = n N_A$ |
| $1$ |
$12$ |
| $2$ |
$24$ |
| $3$ |
$36$ |
| $4$ |
$48$ |
Review - Units of Volume and Pressure
The SI unit for volume is $m^3$. Unit conversion is a very basic skill for a science major. Make sure you know how to convert units to and from $cm^3$ and $L$ (liter) correctly or you will be penalized heavily. Here is a quick reminder:
$$
\begin{eqnarray}
1m &=& 100cm \tag{length}\\
\Rightarrow 1m^2 &=& (100cm)^2 = 10^4 cm^2 \tag{area}\\
\Rightarrow 1m^3 &=& (100cm)^3 = 10^6 cm^3 \tag{volume}\\
\end{eqnarray}
$$
Using the above, we get:
$$
\begin{eqnarray}
1cm^3 &=& 10^{-6} m^3 \\
1L &=& 1000cm^3 = 1000\times 10^{-6}m^3 = 10^{-3} m^3
\end{eqnarray}
$$
The SI unit of pressure is $Pa$ (Pascals), which is equivaldent to $N/m^2$.
A common non-SI unit for pressure is $atm$, or "atmospheric pressure". To convert to SI unit, use $1atm \approx 10^5Pa$.
The term STP stands for standard temperature and pressure, meaning $T=0^\circ C$ and $P=1atm$.
An alternative way of writing the ideal gas law is $PV = NkT$, where $k=1.38\times 10^{-23}J/K$ is the Boltzmann constant. Compare with the version presented above $PV = nRT$, we could see:
$$
\begin{eqnarray}
NkT &=& nRT \\
\Rightarrow Nk &=& nR \\
\Rightarrow k &=& \frac{n R}{N} = \frac{n R}{n N_A} \\
&=& \frac{R}{N_A} \\
&=& 1.38 \times 10^{-23} J/K
\end{eqnarray}
$$
Try It Yourself (click to show)
Question will be loaded by load_exercise_example_all() defined in script_question.js
Question will be loaded by load_exercise_example_all() defined in script_question.js
A useful equation derived from the ideal gas law is:
$$
\frac{P_1 V_1}{T_1} = \frac{P_2 V_2}{T_2}
$$
The implicit assumption here is $n_1 = n_2$. In other words, the container of the box is not leaking so the amount of gas stays constant. For the proof, start with $PV = nRT \Rightarrow nR = \frac{PV}{T}$. The assumption $n_1 = n_2$ then gives the equation above.
Try It Yourself (click to show)
Question will be loaded by load_exercise_example_all() defined in script_question.js
Question will be loaded by load_exercise_example_all() defined in script_question.js
Question will be loaded by load_exercise_example_all() defined in script_question.js