PHYS 170

Lecture 10b - Rotation (torque and angular momentum)

Introduction

In linear motion, acceleration \(a\) is caused by force \(F\). In rotation, angular acceleration \(\alpha\) is caused by torque \(\tau\). The two concepts are best compared side by side:

$$ \begin{eqnarray} F &=& ma \\ \tau &=& I \alpha \end{eqnarray} $$

Torque

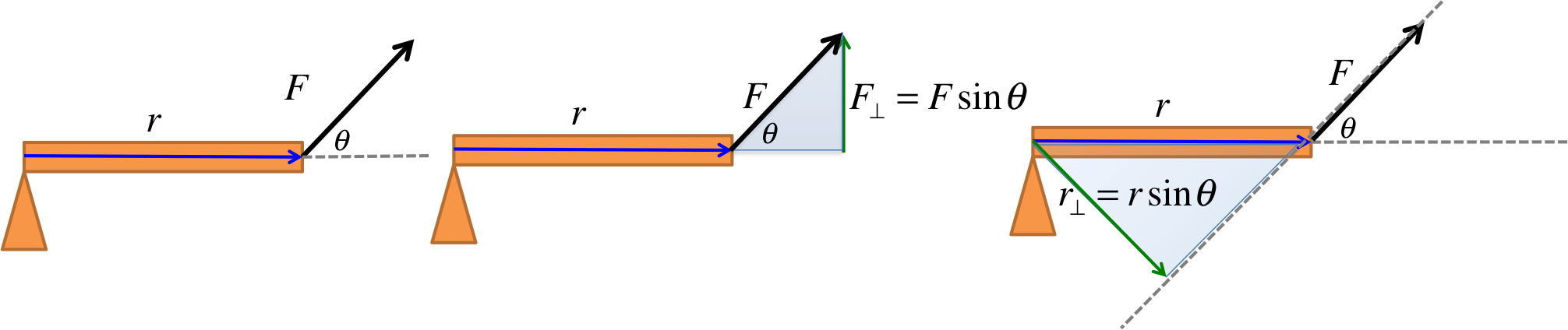
The torque \(\tau\) is defined by:

$$\tau = rF\sin\theta $$
where \(r\) is distance from the axis of rotation to the point of application of the force, and \(\theta\) is the angle between \(r\) and \(F\).

The SI unit for torque is \(Nm\).

Sign convention:
+: counterclockwise torque
-: clockwise torque

Simulation - Torque (click to show)

Canvas not supported
Drag the seesaw to change the angle.
The force can be adjusted by dragging its tip, and it can be moved by dragging its tail.
Calculations will appear here.
Since the forces are all vertical, and the distances are horizontal, the angle \(\theta=90^\circ\). Since \(\sin 90^\circ = 1\), the torque simply reduces to \(\tau = rF\). $$ \begin{eqnarray} \tau_1 &=& +(2m)(10N)= +20Nm \\ \tau_2 &=& -(1.5m)(20N)= -30Nm \\ \tau_{\text{total}} &=& \tau_1 + \tau_2 \\ &=& -10Nm \end{eqnarray} $$ Note that \(\tau_2\) is given a negative sign because \(F_2\) is pushing to cause a clockwise rotation. The net negative torque above means the seesaw will start rotating clockwise.
The angles are no longer \(90^\circ\) after the seesaw tilted \(30^\circ\). From the diagram, one could see that \(\theta_1\) grows by \(30^\circ\) while \(\theta_2\) shrinks by \(30^\circ\): $$ \begin{eqnarray} \theta_1 &=& 90^\circ + 30^\circ = 120^\circ \\ \theta_2 &=& 90^\circ - 30^\circ = 60^\circ \end{eqnarray} $$ $$ \begin{eqnarray} \tau_1 &=& +(2m)(10N)\sin 120^\circ = +17.32Nm \\ \tau_2 &=& -(1.5m)(20N)\sin 60^\circ = -25.98Nm \\ \tau_{\text{total}} &=& \tau_1 + \tau_2 \\ &=& -8.66Nm \end{eqnarray} $$

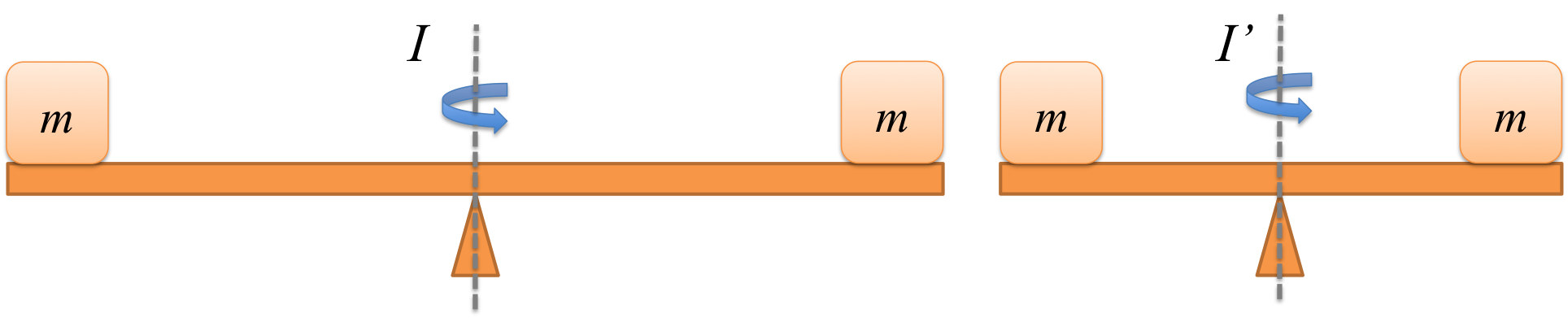
Note that \(\tau_2\) is given a negative sign because \(F_2\) is pushing to cause a clockwise rotation. The net negative torque above means the seesaw will angularly acceleration in the clockwise direction.

Try It Yourself (click to show)

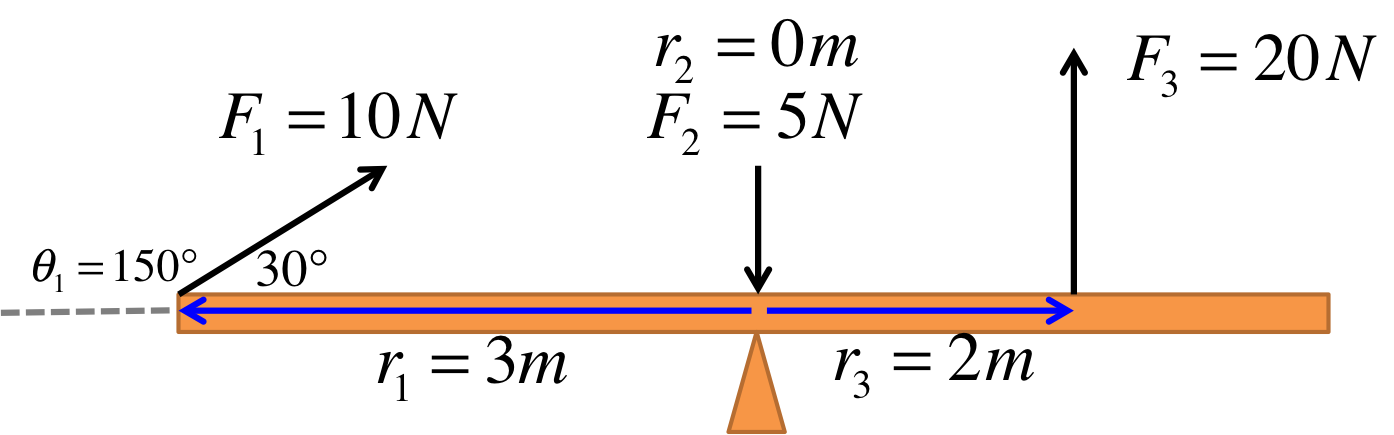
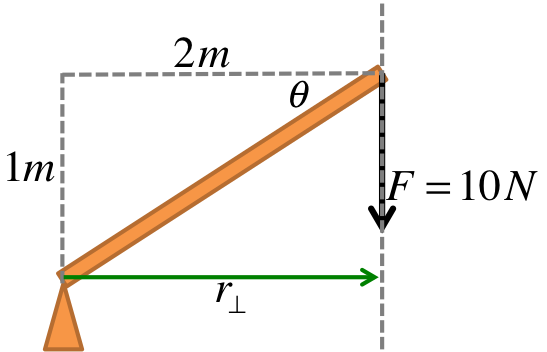
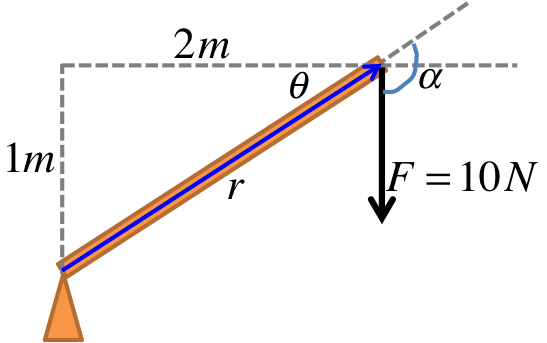
The distances between each force and the axis of rotation are shown in the figure. \(r_2=0m\) because the force is acting directly on the axis of rotation. \(\theta_2\) cannot be defined because the vector \(\vec{r_2}\) vanishes. Also note that technically \(\theta_1 = 150^\circ\) (not \(30^\circ\)). One way to see this is to ask how much you have to rotate \(\vec{r_1}\) before it points in the same direction as \(\vec{F_1}\).

In this simple example, if you had mistakenly used \(\theta_1 = 30^\circ\), you will actually still get the right answer for the torque (in the next exercise) because \(\sin 150^\circ\) and \(\sin 30^\circ\) happen to be the same (due to the trig identity \(\sin\theta = \sin (180^\circ - \theta)\)). However, it is better to be careful because you may not always be so lucky.

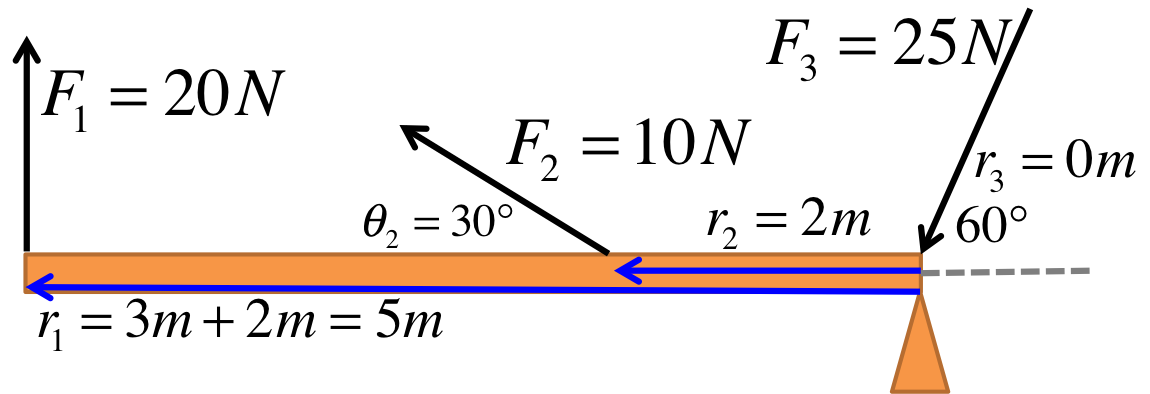
$$ \begin{eqnarray} \tau_1 &=& -(3m)(10N) \sin 150^\circ = -15Nm \\ \tau_2 &=& 0Nm \\ \tau_3 &=& +(2m)(20N)\sin 90^\circ = +40Nm \\ \tau_{\text{total}} &=& -15+0+40 = +25Nm \end{eqnarray} $$
First figure out the distances between the axis of rotation and the forces.

The distances between each force and the axis of rotation are shown in the figure. Pay attention to the direction of the vectors, point from the axis of rotation to where the forces are acting. \(r_3=0m\) because the force is acting directly on the axis of rotation.

Note also that \(r_1=5m\) because you must measure the distance starting from the axis of rotation.

$$ \begin{eqnarray} \tau_1 &=& -(5m)(20N) \sin 90^\circ = -100Nm \\ \tau_2 &=& -(2m)(10N)\sin 30^\circ = -10Nm \\ \tau_3 &=& 0Nm \\ \tau_{\text{total}} &=& -100-10+0 = -110Nm \end{eqnarray} $$
First figure out the distances between the axis of rotation and the forces.
The total torque must be zero for the seesaw to remain balanced. This means the counterclockwise torque (\(\tau_1\)) and clockwise torque (\(\tau_2\)) must have the same magnitude: $$ \begin{eqnarray} |\tau_1| &=& |\tau_2| \\ r_1 F_1 \sin 90^\circ &=& r_2 F_2 \sin 90^\circ \\ r_2 &=& \frac{F_1}{F_2} r_1 \\ &=& \frac{10}{20} (2) = 1m \end{eqnarray} $$

Alternative Forms of Torque

Torque can be calculated in many ways besides the original definition given above:

$$ \begin{eqnarray} \tau &=& rF \sin\theta \\ \tau &=& r_\perp F\\ \tau &=& r F_\perp \end{eqnarray} $$

The variables \(F_\perp\) and \(r_\perp\) are defined in the diagram below. \(F_\perp\) is the component of the force perpendicular to \(\vec{r}\). \(r_\perp\) is the length of the perpendicular line from the axis of rotation to the line defined by \(\vec{F}\).

We will use two different methods to solve this problem.

Method 1 (\(\tau = r_\perp F\))

$$ \begin{eqnarray} r_\perp &=& 2m \\ \Rightarrow \tau &=& -r_\perp F \\ &=& -(2m)(10N) = -20Nm \end{eqnarray} $$ The negative sign is inserted to indicate the clockwise direction of the torque.

Method 2 (\(\tau = r F \sin (angle)\))

We can first find \(r\): $$ r = \sqrt{1^2 + 2^2} = \sqrt{5} = 2.24m $$ The angle \(\theta\) is found as follows: $$ \begin{eqnarray} \tan \theta &=& \frac{1}{2} \\ \theta &=& \tan^{-1} 0.5 = 26.57^\circ \end{eqnarray} $$ At this point, however, it is very important to recognize that \(\theta\) is not the angle between \(r\) and \(F\). The angle we need is the angle \(\alpha\): $$ \alpha = 90^\circ + \theta = 116.57^\circ $$ Only now we have everything we need: $$ \begin{eqnarray} \tau &=& - r F \sin \alpha \\ &=& -(2.24m)(10N)\sin(116.57^\circ) = -20Nm \end{eqnarray} $$
Both methods give the same answer, but clearly in this case method 1 is much faster. One has to be flexible in choosing which method to use.

Newton's Second Law

The rotational version of Newton's Second Law is given by:
$$ \begin{eqnarray} \tau &=& I \alpha \end{eqnarray} $$

Moment of inertial \(I\) and angular acceleration \(\alpha\) were studied in the last lecture.

Try It Yourself (click to show)

Note that the forces are simply \(F_1 = m_1 g\) and \(F_2 = m_2 g\). $$ \begin{eqnarray} I &=& m_1 r_1^2 + m_2 r_2^2 \\ &=& (10)(2^2) + (20)(1.5^2) = 85kgm^2\\ \tau &=& r_1 F_1 \sin 90^\circ - r_2 F_2 \sin 90^\circ \\ &=& (2)(10)(9.8) - (1.5) (20) (9.8) = -98Nm \\ \alpha &=& \frac{\tau}{I} \\ &=& \frac{-98}{85} = -1.15rad/s^2 \end{eqnarray} $$ The negative sign indicates the seesaw will start to rotate clockwise.
block pulled by T
A pulley (\(m = 10kg\)) of radius \(0.2m\) is pulled by a constant force \(F=8N\) and rotates about the central axis. The moment of inertia of a disk is \(I_{\text{disk}} = \frac{1}{2} m r^2\). Find the moment of inertia, the torque, and the angular acceleration about the center.
$$ \begin{eqnarray} I &=& \frac{1}{2} m r_2^2 \\ &=& \frac{1}{2}(10)(0.2^2) = 0.2kgm^2\\ \tau &=& -r F \sin 90^\circ = -(0.2)(8) = -1.6Nm \\ \alpha &=& \frac{\tau}{I} \\ &=& \frac{-1.6}{0.2} = -8rad/s^2 \end{eqnarray} $$ The negative sign indicates the pulley will start to rotate clockwise.

Angular Momentum

The definition of angular momentum \(L\) is:

$$L = I \omega$$

The definition is analogous to that of linear momentum \(p=mv\). The SI unit of angular momenum is \(kgm^2/s\) (which is identical to \(Js\)).

Simulation - Conservation of Angular Momentum (click to hide)

Canvas not supported
Both objects have mass \(m=1kg\) and are separated from the center by distance \(r\). Adjust \(r\) to see how the angular velocity changes, while the total angular momentu stays the same (conservation of angular momentum), obeying \(L = I \omega\).
Note \(I = 2 m r^2\), where the factor of 2 comes from the fact that there are 2 masses on the bar, with each mass contributing \(I_{one\ mass} = m r^2\).
Calculations will appear here.

Try It Yourself (click to show)

block pulled by T
Which objects in the picture has the larger moment of inertia?

\(I = m_1 r_1^2 + m_2 r_2^2\) means larger \(r\) gives larger moment of inertia. In general the further away an object is to the axis of rotation, the larger contribution it will make to \(I\).

An application below: when a skater has her arms sketched out, her momentum of inertial \(I\) is greater than the value \(I'\) when her arms are folded.

Embed from Getty Images
When a skater has her arms sketched out, her momentum of inertial \(I\) is greater than the value \(I'\) when her arms are folded. If \(I = 50kgm^2\) and \(I'=40kgm^2\), and that the skater was spinning at \(\omega = 2rad/s\) in the beginning, what is the final angular velocity when she has her arms folded?
$$ \begin{eqnarray} L &=& L' \\ \Rightarrow I \omega &=& I' \omega' \\ \Rightarrow \omega' &=& \frac{I}{I'} \omega \\ &=& \frac{50}{40} (2) = 2.5rad/s \end{eqnarray} $$

Video - Skater and Angular Momentum (click to show)

Symbol Value
\(m_A\) \( 2kg \)
\(m_B\) \( 4kg \)
Symbol Value
\(r_A\) \( 0.2kg \)
\(r_B\) \( 0.1kg \)
Symbol Value
\(\omega_A\) \( 50rad/s \)
\(\omega_B\) \( 200rad/s \)
Using \(I_{\text{disk}} = \frac{1}{2} m r^2\), we calculate: $$ I_A = 0.04kgm^2, I_B = 0.02kgm^2 $$ Similar to conservation of linear momentum \(m_A u_A + m_B u_B = m_A v_A + m_B v_B\), we have: $$ \begin{eqnarray} I_A \omega_A + I_B \omega_B &=& I_A \omega_f + I_B \omega_f \\ \Rightarrow \omega_f &=& \frac{I_A \omega_A + I_B \omega_B}{I_A + I_B} \\ &=& \frac{(0.04)(50) + (0.02)(200)}{0.04+0.02} \\ &=& 100rad/s \end{eqnarray} $$ The kinetic energy can be found using \(KE = \frac{1}{2} I \omega^2\): $$ \begin{eqnarray} KE_i &=& \frac{1}{2} I_A \omega_A^2 + \frac{1}{2} I_B \omega_B^2 \\ &=& 450J \\ KE_f &=& \frac{1}{2} I_A \omega_f^2 + \frac{1}{2} I_B \omega_f^2 \\ &=& \frac{1}{2} (I_A + I_B) \omega_f^2 \\ &=& 300J \\ \Delta KE &=& KE_f - KE_i \\ &=& -150J \end{eqnarray} $$

Conservation of angular momentum leads to some interesting and sometimes counter-intuitive effects. If you are interested you could watch the videos below to find out more.

Video - Bike Wheel Gyroscope (click to show)

Video - Angular Momentum Demos (click to show)

Notations

Name Symbol Unit Meaning
Torque \(\tau\) \( Nm\) the cause of angular acceleration
Angular momentum \(L\) \( kgm^2/s \) a conserved quantity in rotation