PHYS 170

Lecture 10a - Rotation (kinetic energy and moment of inertia)

Introduction

Starting from this chapter, we will often use radians instead of degrees to measure angles. You need to know how to convert between these two units: $$ \begin{eqnarray} \theta_{\text{radian}} &=& \frac{\pi}{180^\circ} \theta_{\text{degree}} \\ \theta_{\text{degree}} &=& \frac{180^\circ}{\pi} \theta_{\text{radian}} \end{eqnarray} $$

Radian is defined as the ratio of the arc length \(s\) to the radius \(r\): $$ \theta = \frac{s}{r} $$ For example, since for one complete circle \(s=2\pi r\), we get \(\theta = 2\pi\), hence there are \(2\pi\) radians in one circle.

This definition also shows that radian is a "dimensionless unit", meaning that it is the same as 1 (or having no units) because both \(s\) and \(r\) are lengths, their ratio would have no unit. You should treat "\(rad\)" as just a placeholder, so saying \(\theta = 20 rad \) is the same as saying \(\theta = 20\). The same cannot be said for degrees, if you want to say \(\theta = 20^\circ\), you absolutely cannot omit the symbol "\(^\circ\)", otherwise radians will be assumed.

Video - Radian vs Degree Conversion (click to show)

Angular Velocity

Definition

Imagine an object running around the circle, the rate at which the angle \(\theta\) increases is defined to be the angular velocity \(\omega\): $$ \omega = \frac{d\theta}{dt} $$ The unit for angular velocity is \(rad/s\). Note that the symbol for angular velocity is the Greek letter "omega", and not the English letter "w".

For example, if \(\omega = 2rad/s\), it means that the angle increases by \(2rad\) every second.

If it is uniform circular motion (i.e. maintaining the same speed as it runs around the circle), the above equation simplifies to: $$ \omega = \frac{\Delta \theta}{\Delta t} $$

Simulation - The Basics of Rotational Motion (click to hide)

Canvas not supported
Adjust the sliders to see:
  • how long it takes for the object to go around the circle once (period);
  • how many revolutions the object can complete in one second (frequency);
  • how many radians the object can cover per second (angular velocity).

Try It Yourself (click to show)

$$ \begin{eqnarray} \Delta \theta &=& 70^\circ = 70^\circ \times \frac{\pi}{180^\circ} \\ &=& 1.22 rad\\ \Rightarrow \omega &=& \frac{1.22rad}{10s} = 0.12rad/s \end{eqnarray} $$
Since angular velocity is only about the angle covered per unit time, the radius is not needed. There are \(2\pi\) radians in a complete circle, which the object covers in \(10s\): $$ \begin{eqnarray} \omega &=& \frac{2 \pi rad}{10s} = 0.63rad/s \end{eqnarray} $$ The time it takes for an object to complete one cycle is called the period \(T\). In this problem you have just proved one of the equations in the next section, namely: $$ \omega = \frac{2\pi}{T} $$

Other Variables

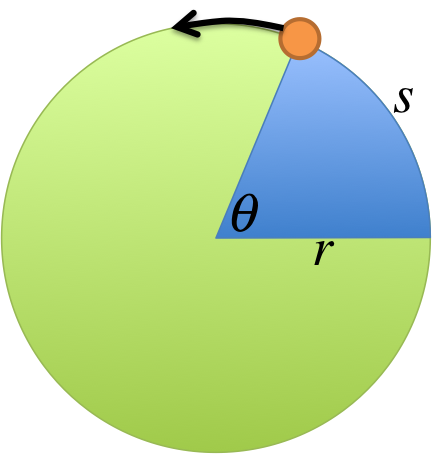
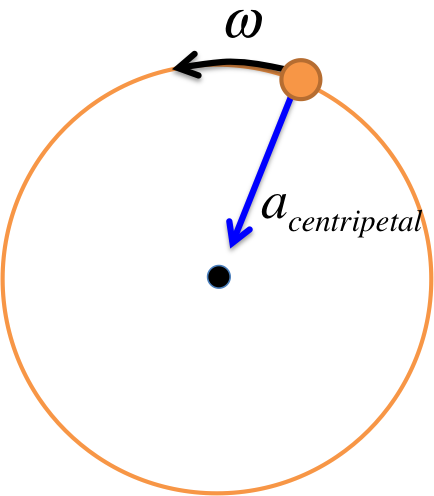
For the rest of the semester, you will need to familiarize yourself with the following variables, which will form the basic vocabulary for the topics to follow.

Name Symbol Unit Meaning
Angular velocity \(\omega\) \( rad/s\) rate of change of angle
Linear (or tangential) speed \(v\) \( m/s \) distance traveled per second
Period \(T\) \(s\) time to complete one cycle
Frequency \(f\) \(Hz = rps\) number of cycles per second

\(rps\) stands for "revolutions per second", which is identical to \(Hz\) and \(s^{-1}\).

Here are the equations that connect the variables together:

$$ \begin{eqnarray} v &=& \omega r\\ \omega &=& \frac{2\pi}{T} &=& 2\pi f \end{eqnarray} $$

You already proved \(\omega = \frac{2\pi}{T}\) earlier in the exercise "angular velocity 3", from this we can show the other equations. We will begin with \(v\). In one period \(T\), the distance traveled should just be the circumference of the circle, i.e. \(2\pi r\). Therefore \(v\), "distance traveled per second", is given by: $$ \begin{eqnarray} v &=& \frac{2\pi r}{T} = \frac{2\pi }{T}r\\ &=& \omega r \end{eqnarray} $$ As for the equation relating \(f\), you could ask the following question: suppose it takes an object \(T=1/2s\) to complete one cycle, how many revolution can it make per second? The answer is 2, so \(f=\frac{1}{T}\). If it takes \(T=1/3s\) for one revolution, how many revolutions can it make per second? Some thinking tells you it would be 3, again giving \(f=\frac{1}{T}\). Since we already know \(\omega = \frac{2\pi}{T}\), we have: $$ \begin{eqnarray} \omega &=& \frac{2\pi}{T} = 2\pi\frac{1}{T}\\ &=& 2\pi f \end{eqnarray} $$

Try It Yourself (click to show)

If it can go around twice in \(40s\), then it takes \(20s\) to go around once, therefore the period \(T\) is \(20s\). $$ \begin{eqnarray} \omega &=& \frac{2\pi}{T} = 0.31 rad/s\\ f &=& \frac{1}{T} = 0.05Hz \\ v &=& \omega r = 0.62m/s \end{eqnarray} $$
The question tells you \(v=0.5m/s\), from this you can find everything else. $$ \begin{eqnarray} \omega &=& \frac{v}{r} = 0.25 rad/s\\ T &=& \frac{2\pi}{\omega} = 25.13 s \\ f &=& \frac{1}{T} = 0.04Hz \end{eqnarray} $$
The question tells you \(v=0.5m/s\), from this you can find everything else. $$ \begin{eqnarray} f &=& 120rpm = \frac{120 rev}{1 min} \\ &=& \frac{120 rev}{60s} = \frac{2 rev}{1s} \\ &=& 2rps = 2Hz \\ \omega &=& 2\pi f = 12.57rad/s \\ T &=& \frac{1}{f} = 0.5 s \\ v &=& \omega r = 25.13 m/s \end{eqnarray} $$
The earth takes 1 day to spin around once, so we know the period is \(T=1day = 86400s\). $$ \begin{eqnarray} \omega &=& \frac{2\pi}{T} = 72.72\times 10^{-6}rad/s \\ f &=& \frac{1}{T} = 11.57\times 10^{-6} Hz \\ v &=& \omega r = (72.72\times 10^{-6})(6.37\times 10^6) = 463.23m/s \end{eqnarray} $$

Centripetal Acceleration

As explained in Chapter 5, while the object on the left undergoes uniform circular motion (meaning its speed stays the same as it goes around), there is a "centripetal acceleration" on the object pointing toward the center given by:

$$ a_{\text{centripetal}} = r \omega^2 = \frac{v^2}{r} $$

Newton's Second Law (\(F=ma\)) tells us the centripetal acceleration must be caused by a force pointing toward the center, called the "centripetal force", given by:

$$F_{\text{centripetal}} = m a_{\text{centripetal}} = \frac{mv^2}{r} = m r \omega^2 $$

Simulation - Centripetal Force (click to hide)

Canvas not supported
Adjust the sliders to see how the trajectory is affected.
Can you calculate the radius of the trajectory?

Video - Centripetal Force (click to show)

Angular Acceleration

Previously we have been considering uniform circular motion. In this section, we will consider cases when the object is speeding up or slowing down at a constant rate. Just like we define linear acceleration as the rate of change of linear velocity, here we define angular acceleration as the rate of change of the angular velocity:

Linear Variable Symbol Unit
Displacement \(s\) \( m \)
Velocity \(v = \frac{ds}{dt}\) \( m/s \)
Acceleration \(a = \frac{dv}{dt}= \frac{d^2s}{dt^2}\) \( m/s^2 \)
Angular Variable Symbol Unit
Angle \(\theta\) \( rad \)
Angular Velocity \(\omega = \frac{d\theta}{dt}\) \( rad/s \)
Angular Acceleration \(\alpha = \frac{d\omega}{dt}= \frac{d^2\theta}{dt^2}\) \( rad/s^2 \)

By analogy we can write down the angular version of the equations of motion you learned in chapter 2:

Linear Equations Missing
\(v = v_0 + at \) \(s\)
\(s - s_0 = v_0t + \frac{1}{2} a t^2 \) \(v\)
\(s - s_0 = \frac{1}{2} (v_0+v)t \) \(a\)
\(v^2 = v_0^2 + 2a(s-s_0) \) \(t\)
Angular Equations Missing
\(\omega = \omega_0 + \alpha t \) \(\theta\)
\(\theta - \theta_0 = \omega_0t + \frac{1}{2} \alpha t^2 \) \(\omega\)
\(\theta - \theta_0 = \frac{1}{2} (\omega_0+\omega)t \) \(\alpha\)
\(\omega^2 = \omega_0^2 + 2 \alpha (\theta-\theta_0) \) \(t\)

Try It Yourself (click to show)

$$ \begin{eqnarray} \theta - \theta_0 &=& \omega_0 t + \frac{1}{2} \alpha t^2 \\ \Rightarrow \theta &=& 5 (10) + \frac{1}{2} (3) (10^2)\\ &=& 200rad \end{eqnarray} $$
$$ \begin{eqnarray} s &=& r \theta \\ &=& (2)(200)\\ &=& 400 m \end{eqnarray} $$

Moment of Inertia

Consider the figure on the left. It shows an object consisting of three balls (\(m_1=1kg, m_2=2kg, m_3=3kg\)), rotating about a vertical axis.

The "moment of inertia" is for this object is: $$ \begin{eqnarray} I &=& m_1 r_1^2 + m_2 r_2^2 + m_3 r_3^2 \\ &=& (1) (4^2) + (2) (3^2) + (3) (3+2)^2\\ &=& 16+ 18 + 75\\ &=& 109kgm^2 \end{eqnarray} $$ \(r\) is defined to be the distance between the mass and the axis of rotation, which explains why \(r_3 = 3+2=5m\).

Moment of inertia is the tendency of an object to remain in its current state of rotational motion (similar to inertia in linear motion, which is the tendency of an object to remain in its current state of motion). Given an non-rotating object, the more moment of inertia it has, the harder it is to rotate the object.

Simulation - Moment of Inertia (click to hide)

Canvas not supported
Drag the objects to different location and use the sliders to adjust their mass.

Try It Yourself (click to show)

The figure gives \(r_1=3+1=4m, r_2=1m, r_3 = 5m\). $$ \begin{eqnarray} I &=& m_1 r_1^2 + m_2 r_2^2 + m_3 r_3^2 \\ &=& (1) (4^2) + (2) (1^2) + (3) (5^2)\\ &=& 93kgm^2 \end{eqnarray} $$
The figure gives \(r_1=0m, r_2=3m, r_3 = 9m\). $$ \begin{eqnarray} I &=& m_1 r_1^2 + m_2 r_2^2 + m_3 r_3^2 \\ &=& (1) (0^2) + (2) (3^2) + (3) (9^2)\\ &=& 18 + 243 \\ &=& 261kgm^2 \end{eqnarray} $$ This example illustrates a very important point, that the value of the moment of inertia depends on the exact position and orientation of the axis of rotation. The larger value of \(I\) compared to the last problem means it is harder to rotate this object about this axis (if the object was not already rotating).
The figure gives \(r_1=3m, r_2=0m, r_3 = 3m, r_4 = 0m\). Since \(m_2\) and \(m_4\) are touching the axis, the distances are zero. Note that we are not trying to find their distance to the center of the cross. $$ \begin{eqnarray} I &=& m_1 r_1^2 + m_2 r_2^2 + m_3 r_3^2 + m_4 r_4^2 \\ &=& (1) (3^2) + (2) (0^2) + (3) (3^2) + (4)(0^2) \\ &=& 9 + 0 + 27 + 0 \\ &=& 36 kgm^2 \end{eqnarray} $$
The figure gives \(r_1=3m, r_2=2m, r_3 = 3m, r_4 = 2m\). In this case, none of the masses are touching the axis of rotation. $$ \begin{eqnarray} I &=& m_1 r_1^2 + m_2 r_2^2 + m_3 r_3^2 + m_4 r_4^2 \\ &=& (1) (3^2) + (2) (2^2) + (3) (3^2) + (4)(2^2) \\ &=& 9 + 8 + 27 + 16 \\ &=& 60 kgm^2 \end{eqnarray} $$

In all the examples earlier, the objects all made up of a small number of point masses. For the geometric shapes below, the values of the moment of inertia are given in the figure on the left.

These equations could be derived by integration, but for the purpose of PHYS 170 you do not need the derivations. You also do not need to memorize these equations because they will be provided to you in the exam. One special case you will see often is that of a disk, which is really just a really thin solid cylinder. According to the figure, we have \(I_{\text{disk}} = \frac{1}{2}MR^2\).

Rotational Kinetic Energy

There are two equations for kinetic energy:

$$ \begin{eqnarray} KE_{\text{linear}} &=& \frac{1}{2} mv^2 \\ KE_{\text{rotational}} &=& \frac{1}{2} I \omega^2 \end{eqnarray} $$

You can think of \(KE_{\text{linear}}\) as the energy due to the translational motion of the center of mass, while \(KE_{\text{rotational}}\) is the energy related to the rotation about some axis. In many problems, both types of kinetic energy are present, in which case you would use: $$KE_{\text{total}} = \frac{1}{2} mv^2+ \frac{1}{2} I \omega^2 $$ An example is a wheel rolling on the ground. The center of mass is going forward (so \(KE_{\text{linear}}\) is non-zero) as it spins about its central axis (so \(KE_{\text{rotational}}\) is non-zero as well).

In the earlier problem, we found \(\omega = 72.72\times 10^{-6}rad/s\). All we need is the moment of inertia: $$ \begin{eqnarray} I &=& \frac{2}{5} M R^2\\ &=& \frac{2}{5} (5.97\times 10^{24}) (6.37\times 10^6)^2 \\ &=& 9.69\times 10^{37}kgm^2\\ \Rightarrow KE_{\text{rotational}} &=& \frac{1}{2} I \omega^2 \\ &=& \frac{1}{2} (9.69\times 10^{37}) (72.72\times 10^{-6})^2 \\ &=& 2.56\times 10^{29} J \end{eqnarray} $$

We will use conservation of energy. We must take into account the fact that it was rolling, meaning both linear \(KE\) and rotational \(KE\) are present:

Position \(PE\) \(KE_{\text{linear}}\) \(KE_{\text{rotational}}\) \(E_{\text{total}}\)
Top \(mgh_1\) \( 0 \) \( 0 \) \(mgh_1\)
Bottom \(mgh_2\) \( \frac{1}{2} m v_2^2 \) \( \frac{1}{2} I \omega_2^2\) \(mgh_2 + \frac{1}{2} m v^2 + \frac{1}{2} I \omega^2\)

Before equating the energy, however, we need to simply the final \(KE_{\text{rotational}}\) in order to express everything in terms of \(v_2\): $$ \begin{eqnarray} KE_{\text{rotational}} &=& \frac{1}{2} I \omega_2^2 \\ &=& \frac{1}{2} (\frac{2}{5} m r^2) (\frac{v_2}{r})^2\\ &=& \frac{1}{5} m v_2^2 \end{eqnarray} $$ This gives:

$$ \begin{eqnarray} mgh_1 &=& mgh_2 + \frac{1}{2} m v_2^2 + \frac{1}{5} m v_2^2 \\ \Rightarrow mgh_1 - mgh_2 &=& \frac{7}{10} m v_2^2\\ \Rightarrow g(h_1 - h_2) &=& \frac{7}{10} v_2^2\\ v_2 &=& \sqrt{\frac{10}{7}g(h_1 - h_2) } \end{eqnarray} $$ Note that \(m\) and \(r\) both canceled out.

Simulation - Rolling Down an Incline (click to hide)

Canvas not supported

Drag on the surface of the incline to change the angle.
The length of the track is \(20m\). The mass of each object is \(1kg\).
\(I_{disk} = \frac{1}{2} m r^2, I_{ring} = m r^2 \).

Activity

Work out the energy of each object at the bottom.
Can you explain why the block arrives at the bottom first, followed by the disc and then the ring?

Try It Yourself (click to show)

$$ \begin{eqnarray} KE_{\text{rotational}} &=& \frac{1}{2} I \omega_2^2 \\ &=& \frac{1}{2} (\frac{1}{2} m r^2) (\frac{v_2}{r})^2\\ &=& \frac{1}{4} m v_2^2 \end{eqnarray} $$
Using \(\frac{1}{4} m v_2^2\) as the final rotational kinetic energy, as found from the last problem: $$ \begin{eqnarray} mgh_1 &=& mgh_2 + \frac{1}{2} m v_2^2 + \frac{1}{2} I \omega_2^2 \\ \Rightarrow mgh_1 &=& mgh_2 + \frac{1}{2} m v_2^2 + \frac{1}{4} m v_2^2 \\ \Rightarrow mgh_1 - mgh_2 &=& \frac{3}{4} m v_2^2\\ \Rightarrow g(h_1 - h_2) &=& \frac{3}{4} v_2^2\\ v_2 &=& \sqrt{\frac{4}{3}g(h_1 - h_2) } \\ &=& \sqrt{\frac{4}{3}(9.8)(10 - 3) } = 9.56m/s \end{eqnarray} $$ We can then use \(\omega = \frac{v}{r}\): $$ \begin{eqnarray} \omega_2 &=& \frac{9.56}{0.5} = 19.13 rad/s \end{eqnarray} $$
Because the block was originally at rest the initial kinetic energy \(KE_1\) is zero. $$ \begin{eqnarray} PE_1 + KE_1 &=& PE_2 + KE_2 \\ \Rightarrow mgh_1 + 0 &=& mgh_2 + \frac{1}{2} mv_2^2 \\ \Rightarrow mgh_1 - mgh_2 &=& \frac{1}{2} mv_2^2 \\ \Rightarrow g (h_1 - h_2) &=& \frac{1}{2} v_2^2 \\ \Rightarrow v_2 &=& \sqrt{2 g (h_1 - h_2)} \\ &=& \sqrt{2 (9.8) (10-3)} = 11.71m/s \end{eqnarray} $$
$$ \begin{eqnarray} PE_1 + KE_1 &=& PE_2 + KE_2 \\ \Rightarrow mgh_1 + \frac{1}{2} mv_1^2 &=& mgh_2 + \frac{1}{2} mv_2^2 \\ \Rightarrow \frac{1}{2} mv_1^2 + mgh_1 - mgh_2 &=& \frac{1}{2} mv_2^2 \\ \Rightarrow \frac{1}{2} v_1^2 + g (h_1 - h_2) &=& \frac{1}{2} v_2^2 \\ \Rightarrow v_2 &=& \sqrt{v_1^2 + 2 g (h_1 - h_2)} \\ &=& \sqrt{6^2 + 2 (9.8) (10-3)} = 13.16m/s \end{eqnarray} $$

Notations

Name Symbol Unit Meaning
Angle (or angular displacement) \(\theta\) \( rad\) angle of the circular path
Angular velocity \(\omega\) \( rad/s\) rate of change of angle
Angular acceleration \(\alpha\) \( rad/s^2\) rate of change of anglular velocity
Linear (or tangential) speed \(v\) \( m/s \) distance traveled per second
Period \(T\) \(s\) time to complete one cycle
Frequency \(f\) \(Hz = rps\) number of cycles per second
Centripetal acceleration \(a_{\text{centripetal}}\) \(m/s^2\) the acceleration of an object undergoing uniform circular motion
Centripetal force \(F_{\text{centripetal}}\) \(N\) the force that keeps an object in circular orbit
Moment of inertia \(I\) \(kg\cdot m^2\) the tendency to remain in an object's current state of rotational motion