Introduction
Momentum is defined by: $$ p = mv $$ In a collsion the total momentum of the system is conserved. The SI unit of momentum is \(kgm/s\) or \(Ns\).
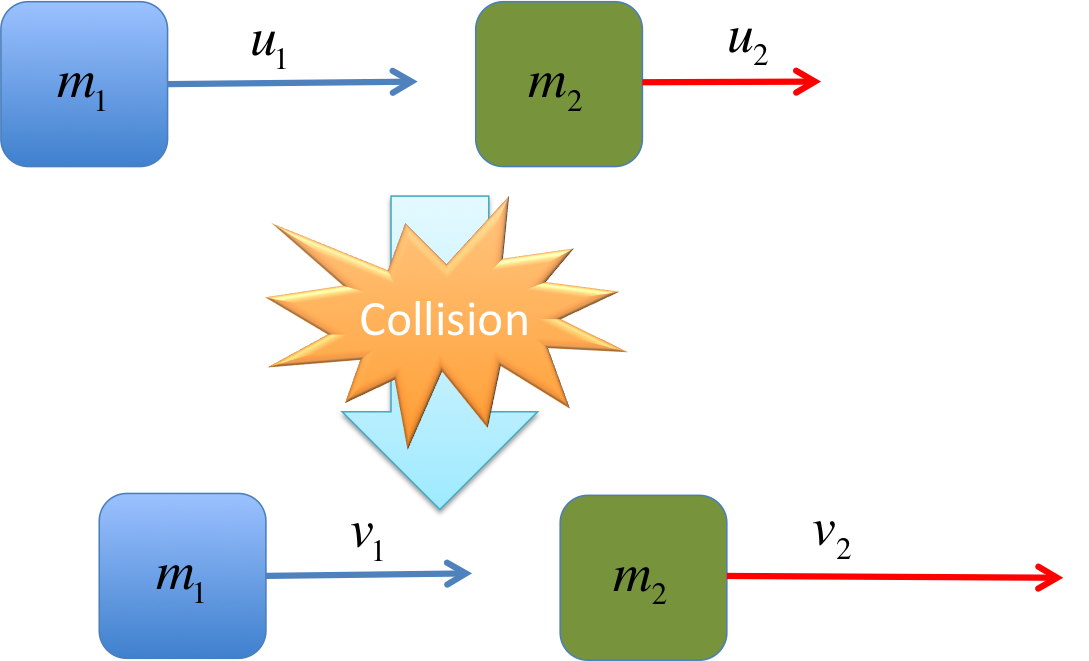
Applied to the picture above, the law of conservation of momentum is:
Lecture 08 - Momentum and Collision
Momentum is defined by: $$ p = mv $$ In a collsion the total momentum of the system is conserved. The SI unit of momentum is \(kgm/s\) or \(Ns\).

Applied to the picture above, the law of conservation of momentum is:
We will study two types of collisions:
| Name | Definition | After collision | Equation |
|---|---|---|---|
| Elastic collision | \(KE_i = KE_f\) | objects separate cleanly | \(\frac{1}{2} m_1 u_1^2 + \frac{1}{2} m_2 u_2^2 = \frac{1}{2} m_1 v_1^2 + \frac{1}{2} m_2 v_2^2 \) |
| Inelastic collision | \(KE_i \neq KE_f\) | objects stick together | \(v_1 = v_2\) |
In other words, in an elastic collision, the system retains all its kinetic energy from before the collision. While in an inelastic collision, some of the kinetic energy is lost and is converted into heat and other forms of energy that are not kinetic. In the macroscopic world, there is no perfect elastic collision because some kinetic energy is always lost. Similarly, the condition \(v_1 = v_2\) actually only applies to what is known as "totally inelastic collision" when the objects completely stick together. Most collisions are in-between cases, but we will not worry about such partially elastic collisions in this course.
No matter what type of collision it is, conservation of momentum (\(m_1 u_1 + m_2 u_2 = m_1 v_1 + m_2 v_2\)) still applies.
Do not use conservation of energy to solve collision problems because generally some energy of the colliders is lost to the surroundings during the collision.
We start with two equations: $$ \begin{eqnarray} m_1 u_1 + m_2 u_2 &=& m_1 v_1 + m_2 v_2 \tag{conservation of momentum}\\ \frac{1}{2} m_1 u_1^2 + \frac{1}{2} m_2 u_2^2 &=& \frac{1}{2} m_1 v_1^2 + \frac{1}{2} m_2 v_2^2 \tag{definition of elastic collision} \end{eqnarray} $$ Now we have two equations, and only two unknows (\(m_2, v_2\)).
Put the numbers in the first equation: $$ \begin{eqnarray} m_1 u_1 + m_2 u_2 &=& m_1 v_1 + m_2 v_2\\ \Rightarrow (4)(2) &=& (4)(-1) + m_2 v_2 \\ \Rightarrow m_2 v_2 &=& 12 \end{eqnarray} $$ The second equation gives: $$ \begin{eqnarray} \frac{1}{2} m_1 u_1^2 + \frac{1}{2} m_2 u_2^2 &=& \frac{1}{2} m_1 v_1^2 + \frac{1}{2} m_2 v_2^2 \\ \Rightarrow \frac{1}{2} (4) (2)^2 &=& \frac{1}{2} (4) (-1)^2 + \frac{1}{2} m_2 v_2^2 \\ \Rightarrow 8 &=& 2 + \frac{1}{2} m_2 v_2^2 \\ \Rightarrow m_2 v_2^2 &=& 12 \\ \end{eqnarray} $$ This gives the following equations: $$ \begin{eqnarray} m_2 v_2 &=& 12 \\ m_2 v_2^2 &=& 12 \end{eqnarray} $$ The first one gives \(m_2 = \frac{12}{v_2}\), putting it into the second one we have: $$ \begin{eqnarray} (\frac{12}{v_2})v_2^2&=& 12\\ v_2 &=& 1 m/s \\ \Rightarrow m_2 &=& \frac{12}{v_2} = 12kg \end{eqnarray} $$
"Impulse" measures an amount of force applied over a period of time. If the time duration (\(\Delta t\)) of the force is short (which is typical of collisions), we can write impulse as: $$ I \approx F \Delta t $$ The unit of impulse is \(Ns\), which is actually identical to \(kgm/s\), the unit of momentum. (The general equation of impulse is actually \(I = \int F dt\), but the approximation above will be good enough for the study of collisions in this course.)
The main result concerning impulse is the following: $$ I = \Delta p $$ In other words, the impulse applied to an object will determine its change of momentum. Intuitively this makes sense because the harder you push and the longer you push (i.e. larger \(F\Delta t\)), the more you could change the motion of an object. This could be proven mathematically using Newton's Second Law: $$ \begin{eqnarray} F&=&ma \\ &=& m \frac{dv}{dt} = \frac{d (mv)}{dt} \\ &=& \frac{dp}{dt} \\ \Rightarrow F &\approx& \frac{\Delta p}{\Delta t} \\ \Rightarrow F \Delta t &\approx& \Delta p \\ \Rightarrow I &\approx& \Delta p \end{eqnarray} $$
Imagine you throw out a stick in a spinning motion (in the absence of gravity):

The motion looks really complicated. However, with the help of a special point, the center of mass, represented by a red dot below, the motion above could be separated into 2 simple motion:
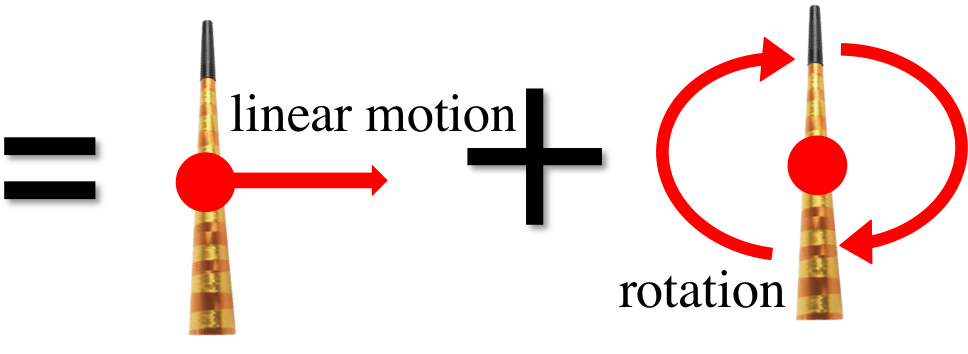
Center of mass enables us to split complicated motion into linear motion and rotation, which we can then calculate separately.
Here is another example, in the presence of gravity:
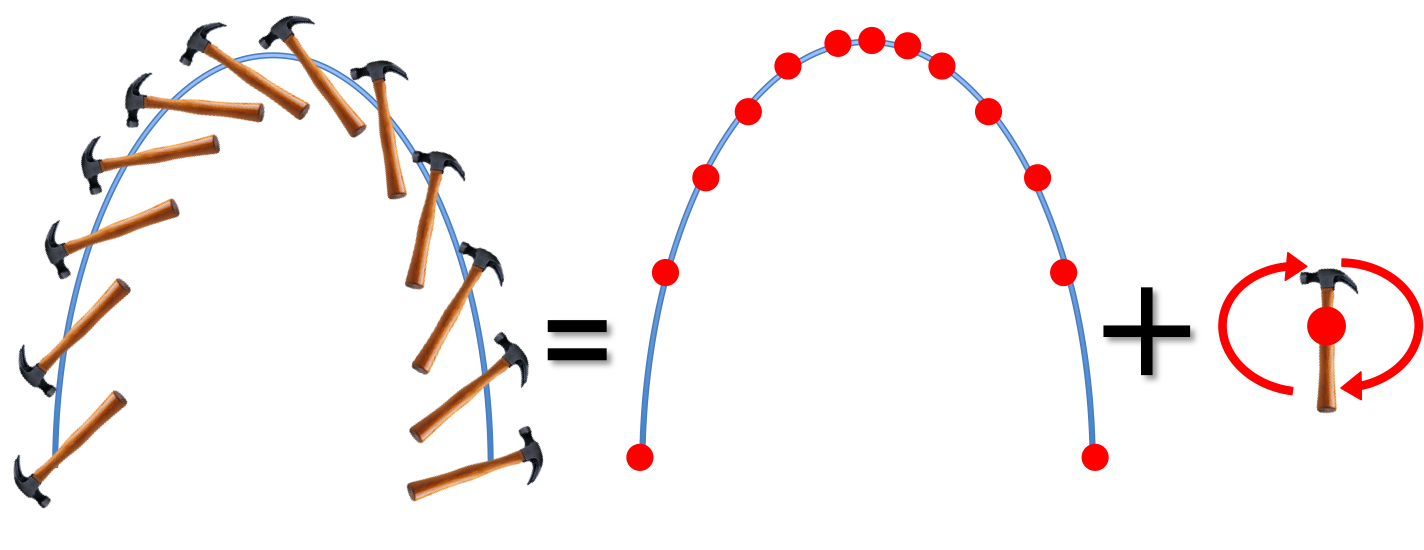
You already learned in an earlier chapter how to compute the motion of a point mass in projectile motion, once you learn (in the next few chapters) how to compute the rotation of the hammer, you will be able to describe the complicated motion of the hammer and any other big (non-point-like) objects completely.
The basic formula for the center of mass is:
The formula could be easily generalized to three or more masses, and in higher dimensions. For example, the center of mass of three objects along the \(x\) and \(y\) axis are: $$ x_{CM} = \frac{m_1 x_1 + m_2 x_2 + m_3 x_3}{m_1 + m_2 + m_3}\\ y_{CM} = \frac{m_1 y_1 + m_2 y_2 + m_3 y_3}{m_1 + m_2 + m_3} $$
In summary the center of mass is at: $$ (2, 2.5)m $$
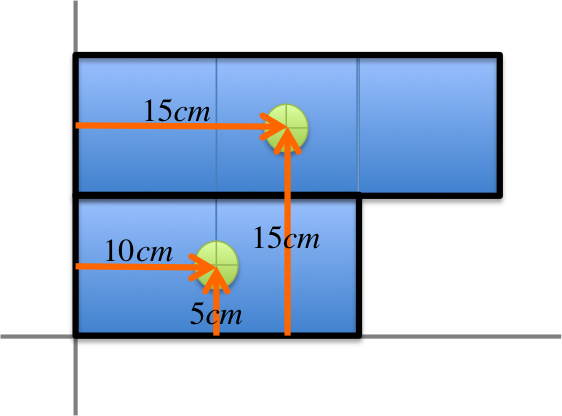
The mass of each square is not given, so we will assume each to have mass \(M\) (which will be canceled out in the calculation below). The main trick here is to group a few squares together and replace the group by their center of mass, as in the figure on the left.
This turns the object into these two point masses at positions: $$ \begin{eqnarray} 3M: (15, 15) \\ 2M: (10, 5) \end{eqnarray} $$ From this it is now straight forward to find the center of mass: $$ \begin{eqnarray} x_{CM}&=& \frac{(3M)(15)+(2M)(10)}{3M+2M} \\ &=& \frac{65M}{5M} = 13cm\\ y_{CM}&=& \frac{(3M)(15)+(2M)(5)}{3M+2M} \\ &=& \frac{55M}{5M} = 11cm \end{eqnarray} $$
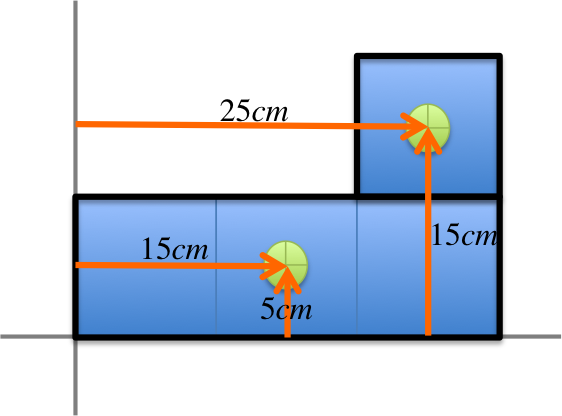
The mass of each square is not given, so we will assume each to have mass \(M\). The main trick here is to group a few squares together and replace the group by their center of mass, as in the figure on the left.
This turns the object into these two point masses at positions: $$ \begin{eqnarray} 1M: (25, 15) \\ 3M: (15, 5) \end{eqnarray} $$ From this it is now straight forward to find the center of mass: $$ \begin{eqnarray} x_{CM}&=& \frac{(M)(25)+(3M)(15)}{M+3M} \\ &=& \frac{70M}{4M} = 17.5cm\\ y_{CM}&=& \frac{(M)(15)+(3M)(5)}{M+3M} \\ &=& \frac{30M}{4M} = 7.5cm \end{eqnarray} $$
Center of mass can be used to prove conservation of momentum. While the arguement could be made mathematically rigorous, we will simply point out the rough idea here.
Suppose two masses \(m_1\) and \(m_2\) are about to collide, their combined center of mass will not be affected by interactions between the two masses. If for the duration of their collision there is negligible external force, then the center of mass will essentially behave like a point object described in Newton's First Law, traveling at constant velocty (this can be seen in the simulation Collision and Conservation of Momemtum above, click on the "Show CM" button to see): $$ v_{CM} = constant $$ But the center of mass velocity \(v_{CM}\) is just the time derivative of the position of the center of mass: $$ \begin{eqnarray} constant&=& v_{CM} = \frac{dx_{CM}}{dt} \\ &=& \frac{d}{dt} (\frac{m_1 x_1+m_2 x_2}{m_1+m_2}) \\ &=&\frac{m_1 \dot{x_1}+m_2 \dot{x_2}}{m_1+m_2} \\ &=& \frac{m_1 v_1+m_2 v_2}{m_1+m_2} \\ \Rightarrow m_1 v_1+m_2 v_2 &=& constant \end{eqnarray} $$ The last line is the law of conservation of momemtum.
| Name | Symbol | Unit | Meaning |
|---|---|---|---|
| Momentum | \(p\) | \( kgm/s = Ns\) | a quantity conserved in collisions |
| Impulse | \(I\) | \( Ns = kgm/s\) | a measure of how hard you push and for how long, leads to change in momentum |