PHYS 170

"Work" means energy transfer.

When you kick a football, you are transfering your energy to the ball. You can say either "you do work on the football", or "work is done on the football by you". The common notation of work is \(W\), and the SI unit is \(J\) (Joules), the same unit as energy.

The basic formula for work:

\(W\) could be positive, zero, or negative, depending on the angle \(\theta\):

The three cases could be seen here:

Intuitively, the \(W>0\) case is when the force is speeding up the object, therefore transfering energy to the object. In the second case \(W=0\) because perpendicular directions decouple, meaning the vertical force cannot affect the horizontal speed so no energy is transferred. The \(W< 0\) case is when the force is opposing the movement of the object and slowing it down, therefore taking energy away.

Useful fact: \(\cos 180^\circ = -1 \), and \(\cos 90^\circ = 0 \).

Try It Yourself (click to show)

The angle between the displacement of the rain drop and air resistance is \(180^\circ\), therefore: $$ \begin{eqnarray} W_{resistance} &=& F_{resistance} s \cos(180^\circ) \\ &=& (0.013N)(10m)(-1) \\ &=& -0.13J \end{eqnarray} $$ Note that \(1J = 1Nm\).

The angle between the displacement of the rain drop and gravity is \(0^\circ\), therefore: $$ \begin{eqnarray} W_{gravity} &=& F_{gravity} s \cos 0^\circ = mg s \cos 0^\circ \\ &=& (0.002kg)(9.8m/s^2)(10m)(1) \\ &=& 0.196J \end{eqnarray} $$ Note that \(1J = 1Nm\).

Four forces are acting on an object. Find their work done on the object using the numbers show in the figure on the left.

Look at the angles carefully. They are not all \(20^\circ\)! Some forces are helping the object to move faster (\(W> 0\)), some of them are slowing it down (\(W< 0\)).

$$ \begin{eqnarray} W_A &=& F_A s \cos 0^\circ = 15J \\ W_B &=& F_B s \cos 20^\circ = 23.49J \\ W_C &=& F_C s \cos 180^\circ = -35J \\ W_D &=& F_D s \cos 160^\circ = -9.4J \end{eqnarray} $$ The sign of \(W\) tells us \(F_A, F_B\) are giving the object energy, moving it faster, but \(F_C, F_D\) are taking energy away, slowing it down. The total work is given by: $$ W_{total} = W_A + W_B + W_C + W_D = -5.91J $$ The negative total means the object is losing energy overall and is slowing down as a result.

The figure shows all the forces acting on the object. We can see that both the force of gravity and the normal force are perpendicular to the displacement. Since \(\cos 90^\circ = 0\), both work must be zero. Mathematically, we have: $$ \begin{eqnarray} W_g &=& mg s \cos 90^\circ = 0J \\ W_N &=& F_N s \cos 90^\circ = 0J \end{eqnarray} $$ The zero result shows that gravity and normal force do not transfer energy either into or out of the chest.

Even though the original description of never mentions "friction", one could deduce the existence of friciton indirectly based on the fact that the chest is moving at constant velocity. If there had been no friction, the horizontal component of \(F_1\) would have caused an acceleration, but since \(a=0m/s^2\), we know that friction \(f\) must be present.

After decomposing \(F_1\), we redraw the force diagram by replacing \(F_1\) with its components. For \(a_x=0m/s^2\), the horizontal forces must cancel out: $$ \begin{eqnarray} f &=& F_1 \cos 60^\circ \\ &=& 100N \cos 60^\circ = 50N \end{eqnarray} $$

Try It Yourself (click to show)

From the picture on the left, we could see that the angle between the displacement and the force of gravity is given by: $$ 90^\circ + \theta = 110^\circ $$ The zero result shows that gravity and normal force do not transfer energy either into or out of the chest.

We learned from the last problem that the angle between displacement and gravity is \(110^\circ\), therefore: $$ \begin{eqnarray} W_g &=& mg s \cos 110^\circ \\ &=& (10)(9.8)(8) \cos 110^\circ \\ &=& -268.14 J \end{eqnarray} $$ The negative answer means gravity is taking energy from the box as it is being pulled up. It makes sense because gravity is definitely working against you pulling the box up. A (wrong) positive answer will imply that gravity is actually helping the box move up, contradicting common sense.

The angle between displacement and friction is \(180^\circ\), therefore: $$ \begin{eqnarray} W_f &=& f s \cos 180^\circ \\ &=& (12)(8) (-1) \\ &=& -96 J \end{eqnarray} $$ The ansewr is negative because friction is taking energy away from the object.

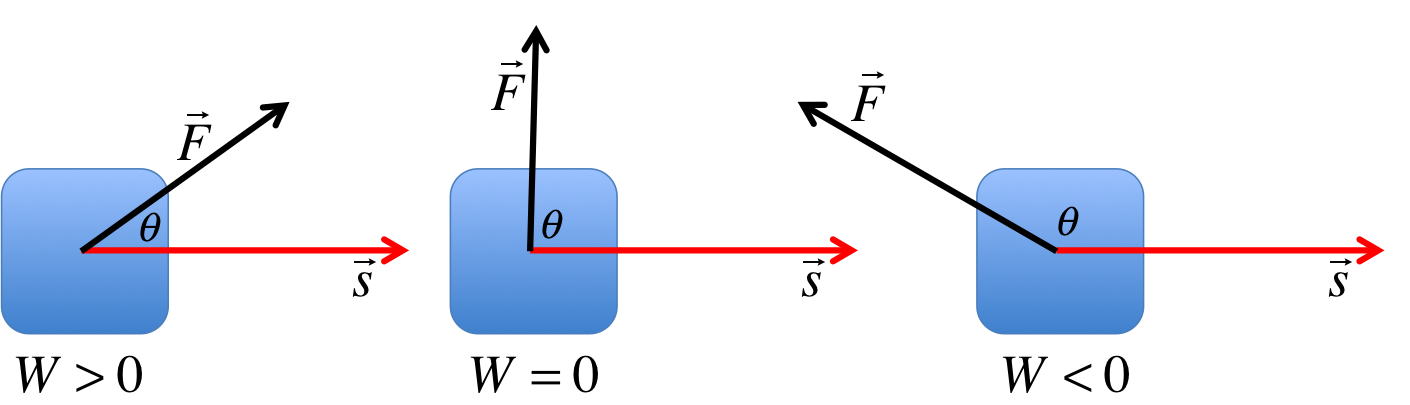
Kinetic energy is the energy of motion: $$ KE = \frac{1}{2}mv^2 $$ The faster, the more massive the object is, the more kinetic energy it carries.

Energy is always a scalar (not a vector), the \(v\) inside the equation of \(KE\) is actually just the speed (magnitude of the velocity vector), i.e. \(v=|\vec{v}|\). It means the direction of the velocity does not affect its \(KE\). An object traveling \(10m/s\) west has exactly the same \(KE\) as an object traveling at \(10m/s\) east.

Kinetic energy and work are related to each other via the work-kinetic-energy theorem:

The theorem can be easily understood as long as you remember "work" means "energy transfer". When an object receives energy transfer from forces acting on it, the transferred amount (work) turns into its kinetic energy.

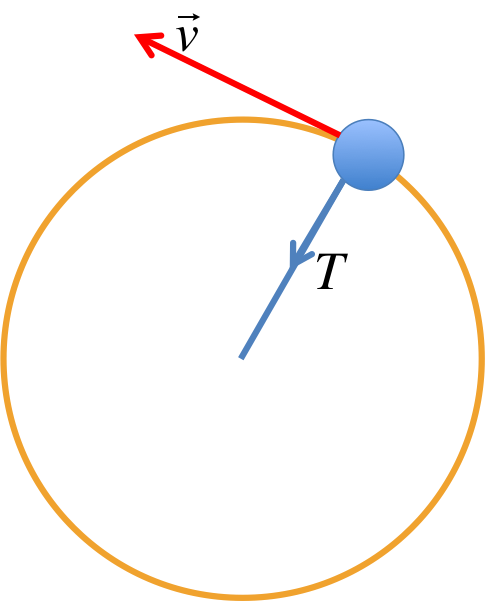
A special case is when \(W_{total} = 0J\). This means no energy transfer is taking place, and not surprisingly means there is no change in kinetic energy: $$ \Delta KE = W_{total} = 0J $$ This means that the object will travel with no change in speed.

Try It Yourself (click to show)

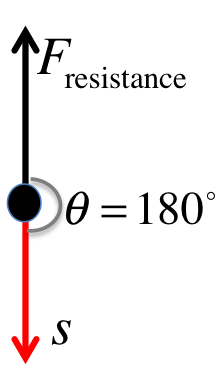
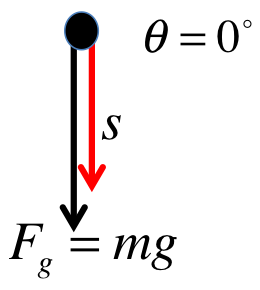
$$ \begin{eqnarray} W_{resistance} &=& F_{resistance} s \cos 180^\circ \\ &=& (30)(10)(-1) = -300J \\ W_{g} &=& mg s \cos 0^\circ \\ &=& (4)(9.8)(10)(1) = 392J \\ W_{total} &=& -300 + 392 = 92J \end{eqnarray} $$

$$ \begin{eqnarray} KE_i &=& \frac{1}{2}mv_i^2 \\ &=& \frac{1}{2} (4) (6^2) = 72J \\ KE_f &=& KE_i + \Delta KE \\ &=& KE_i + W_{total} \\ &=& 72 + 92 = 164 J \\ \frac{1}{2}mv_f^2 &=& KE_f \\ \Rightarrow v_f &=& \sqrt{\frac{2 KE_f}{m}} \\ &=& \sqrt{\frac{2 (164)}{4}} = 9.06m/s\\ \end{eqnarray} $$

"Power" means the rate of work, SI unit is \(W\) (Watts): $$ P = \frac{dW}{dt} $$ Note that \(1W = 1J/s\). A light bulb running at power of \(100W=100J/s\) means that it consumes \(100J\) of energy per second.

Substituting in \(W=F s \cos\theta \) gives: $$ \begin{eqnarray} P &=& \frac{d (F s \cos\theta )}{dt} \\ &=& F \cos\theta \frac{ds}{dt} \\ &=& F v \cos\theta \end{eqnarray} $$

The figure on the left shows a ball tied by a string flying around in uniform circular motion (ignore gravity and friction in this example). The string has tension \(T\), and yet the power is zero, i.e. \(P=0\). This is because the angle between the velocity and the tension is always \(90^\circ\) (recall \(\cos 90^\circ =0\)), so no energy is transferred into the ball. This means the ball does not gain energy from \(T\) and therefore will continue to fly at the same speed (\(\Delta KE = 0J\)).

Knowing \(1W=1J/s\) allows us to define a non-SI unit to measure energy, the kilowatt-hour. \(1kWh\) can be thought of as the energy consumed by a \(1kW=1000W\) light bulb in one hour. This definition means we can convert \(1kWh\) back into \(J\) as follows: $$ \begin{eqnarray} 1kWh &=& (1000W)(1h) = (1000J/s)(3600s) \\ &=& 3.6\times 10^6 J \end{eqnarray} $$ The unit is commonly seen on the electricity bill. The current rate is about \($0.30\) per \(kWh\).