Lecture 04a - Newton's Laws

Introduction

Newton's Laws of Motion (the very brief version):

velocity is either zero or constant when net force is zero.
$F=ma$
action = reaction, but in the opposite direction.

"Net force" means the total force you get after adding all the forces together as vectors. For example, if you have a $5N$ -force pointing left, a $2N$ -force pointing right, the net force is not $7N$ , but $3N$ pointing left. Mathematically, the net force is found by: $\vec{F_{net}} = (-5\hat i) + (2\hat i) = -3\hat i N$ Never calculate the net force by summing up the magnitudes without taking the direction into account.

A Brief Video Introduction on Newton's Laws (click to show)

The First Law

Inertia and Mass

Newton's First Law is also known as the law of inertia.

Inertia is the tendency of an object to remain at rest or in motion with constant speed along a straight line.
Mass is a number that measures an object's inertia. In short, you can think "mass = inertia".

A moving ice puck moving on very smooth ice will keep moving because it has the tendency to remain in motion with constant speed, in other words because it has inertia.

Image by Santeri Viinamäki [CC BY-SA 4.0], via Wikimedia Commons

Mass vs Weight

In physics, mass and weight are not the same thing.

Difference	Mass	Weight
Meaning	measures inertia, an intrinsic property that does not change	gravitation force, value changes depeding on the strength of the gravitational field
Example	you have the same mass on earth or on the moon	you weigh less on the moon than on earth
Unit	$kg$	$N$

The basic equation of weight is: $F_{gravity} = mg$ where $g$ is the acceleration due to gravity. Since weight is just the name for the force of gravity, we used the notation " $F_{gravity}$ ". Other common notations for weight are $W, F_g$ , and in many cases we will simply write " $mg$ " for weight. Also note how the unit matches on both sides because $1N = 1kg m/s^2$ .

Try It Yourself (click to show)

Exercise - weight on earth and on the moon

Given $g_{earth} = 9.8m/s^2$ and $g_{moon} = 1.8m/s^2$ , what is the weight of a $70kg$ -man on the earth and on the moon?

$W_{earth}=$
$W_{moon}=$

Select unit:

$kg$

$W$

$m/s^2$

$N$

Use

$F_{gravity} = mg$ .

Feedback will appear here.

Exercise - plane at constant velocity

A plane is flying forward at a constant velocity. What is the direction of the net force on it?

Solution

The First Law states that no net force is necessary to move at constant velocity.

Down

Forward

No net force

Feedback will appear here.

The Third Law

Newton's Third Law states that for every action (force), there is an equal and opposite reaction. In other words you cannot push without being pushed back just as hard. In a later chapter, you will see how the Third Law leads to the law of conservation of momemtum during collisions.

Video on the Third Laws (click to show)

Opposing Forces

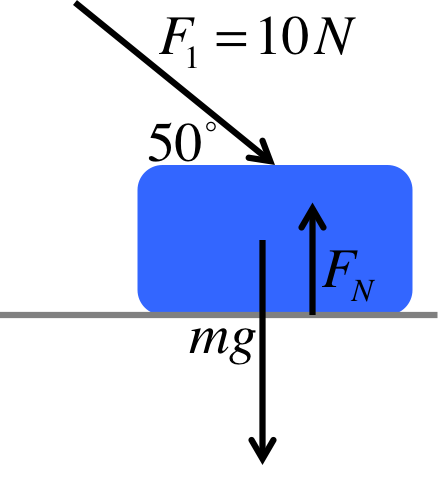
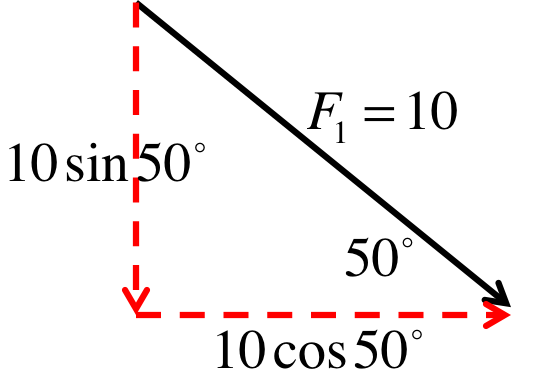
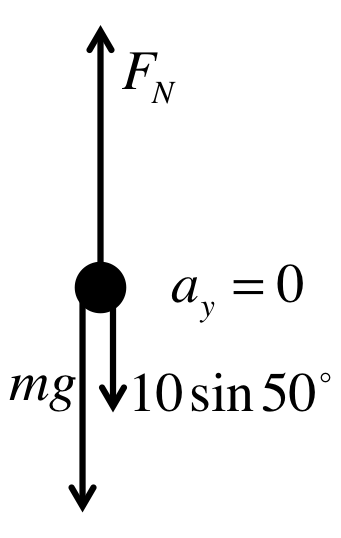Most of the problems you do will involve more than one forces, all point in different directions. It is essential that you know how to deal with this situation correctly. There are many methods to do this, but I will teach you one that is the easiest to apply to problems you see in this course.

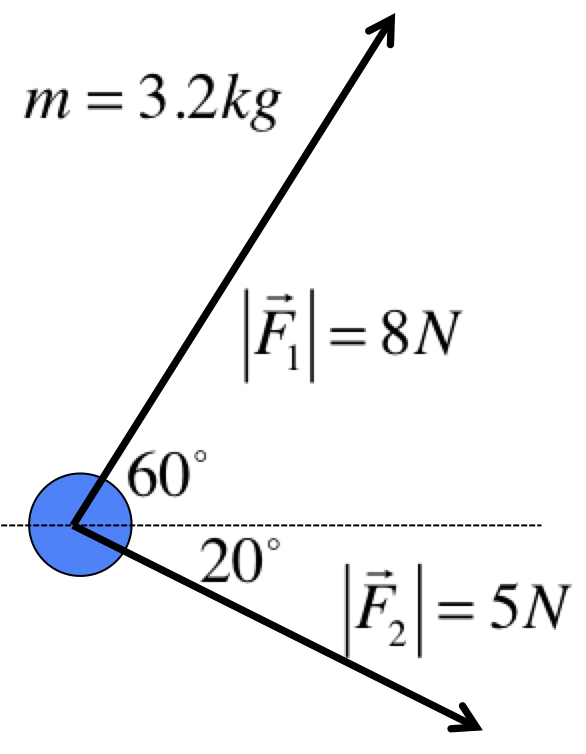
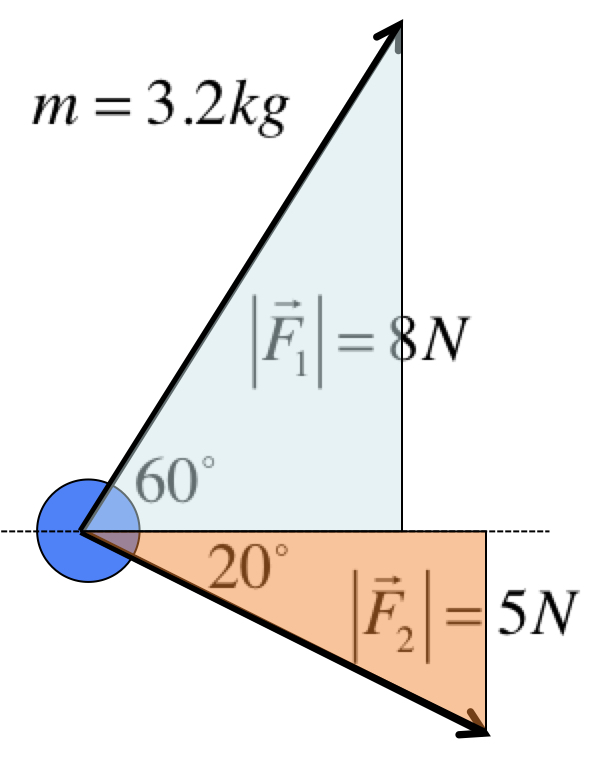
Below shows the two possibilities you have to learn about:

(a)

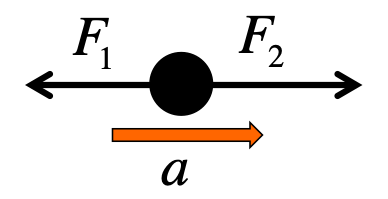
(b)

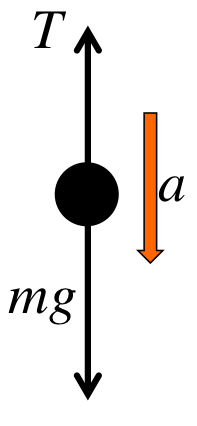
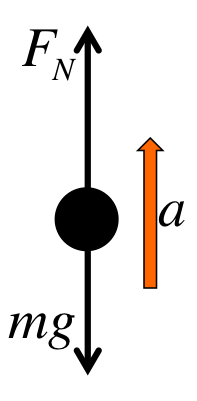
These are called "free-body diagrams", or "force diagrams". Each is a dot with arrows coming out of it. The "dot" represents the mass, while each arrow is a force. On the outside, you could use another arrow to denote the acceleration.

In our convention, every variable on the force diagram represents only the magnitude, so they are all positive. We let the arrows represent the directions, and we do not use negative numbers, even if they point left or down. Do not use the "up is positive, down is negative" convention we had in chapter 1 and 2.

With this convention, this is how you apply the Second Law:

$\begin{eqnarray} (\text{forces in the same direction as }a) - (\text{forces in the opposite direction to }a) &=& ma \\ \text{Or symbolically: } F_{same}-F_{opposite} &=& ma \end{eqnarray}$

Again, the

$a$ and the

$F$ in this equation are magnitudes so they will all be positive numbers in this convention.

Example - horizontal opposing forces

Find the magnitude of the acceleration based on Figure (a) and (b) above. You can use $m$ to denote the mass.

Solution

(a) Since

$F_1$ is opposite to

$a$ and

$F_2$ is in the same direction as

$a$ , we have:

$\begin{eqnarray} F_{2}-F_{1} &=& ma \\ \Rightarrow a &=& \frac{F_2-F_1}{m} \end{eqnarray}$

(b) Since

$F_1$ is same direction as

$a$ and

$F_2$ is opposite to

$a$ , we have:

$\begin{eqnarray} F_{1}-F_{2} &=& ma \\ \Rightarrow a &=& \frac{F_1-F_2}{m} \end{eqnarray}$

Be very careful with the order of the forces. If you reversed them you will get the wrong answer.

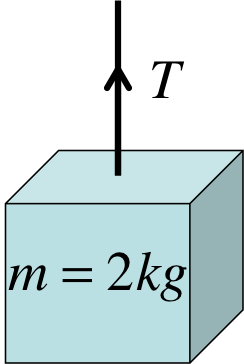
Example - a block pulled vertically by two opposing forces (upward $a$ )

$2kg$ block is being accelerated upward at

$4m/s^2$ by a cable. Find the tension

$T$ in the cable.

Solution

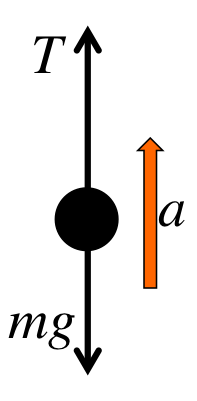
First you must start with a force diagram. There are two forces, the tension

$T$ and the weight of the object

$mg$ . The question states the acceleration is upward so it is indicated in the diagram.

$\begin{eqnarray} F_{same}-F_{opposite} &=& ma \\ \Rightarrow T - mg &=& ma \\ \Rightarrow T &=& mg+ma = m(g+a) \\ &=& (2)(9.8 + 4) = 27.6N \end{eqnarray}$ Note that tension is a force, so it is measured in

$N$ just like all forces.

Try It Yourself (click to show)

Exercise - a block pulled vertically by two opposing forces (downward $a$ ) 2

Continue from the last example. If the block is accelerating downward at $4m/s^2$ , which equation do we obtain when we apply Newton's Second Law?

Draw a force diagram first. The acceleration is now pointing downward (instead of up like the example). Of the two forces

$T$ and

$mg$ , which is in the same direction as

$a$ , which is opposite?

Solution

First you must start with a force diagram. There are two forces, the tension

$T$ and the weight of the object

$mg$ . The question states the acceleration is downward so it is indicated in the diagram. In this case,

$mg$ is in the same direction as

$a$ but

$T$ is opposite.

$\begin{eqnarray} F_{same}-F_{opposite} &=& ma \\ \Rightarrow mg - T &=& ma \end{eqnarray}$

$T-mg=ma$

$mg-T=ma$

Feedback will appear here.

Exercise - a block pulled vertically by two opposing forces (downward $a$ ) 3

Based on the equation you obtained from the last problem, find the tension $T$ when the block is accelerating downward at $4m/s^2$ .

Select unit:

$m$

$m/s^2$

$N$

$kg$

Just solve the equation you obtained from the last problem for

$T$ .

Solution

$\begin{eqnarray} mg - T &=& ma \\ \Rightarrow T &=& mg-ma = m(g-a) \\ &=& 2(9.8-4) = 11.6N \end{eqnarray}$

Feedback will appear here.

Exercise - a block pulled vertically by two opposing forces (zero $a$ ) 4

What is the tension $T$ if the block is moving upward at a constant velocity of $4m/s$ .

Select unit:

$m$

$m/s^2$

$N$

$kg$

What should the net force be if a mass is not accelerating?

Solution

If there is no acceleration, the two opposing forces must cancel out. This means they must have the same magnitude:

$\begin{eqnarray} T &=& mg \\ \Rightarrow T &=& 2(9.8) = 19.6N \end{eqnarray}$

Feedback will appear here.

Multiple Forces

Example - normal force and a pulling force

$2kg$ block is pulled by a

$10N$ force at

$20^\circ$ on a frictionless surface as shown. Assuming the block slides on the surface without being lifted off, find the normal force on the block.

Solution

First identify all the forces in the problem, as shown on the left.

Since the normal force

$F_N$ is vertical, we need to identify all the vertical forces so we have to find the vertical component of

$F_2$ . We can ignore the horizontal component for this problem because vertical forces and horizontal ones do not affect each other.

Draw only the vertical forces in a force diagram. Since the block has no vertical movement, the vertical acceleration

$a_y$ is zero. This means all the vertical forces must cancel out:

$\begin{eqnarray} F_{up} &=& F_{down} \\ \Rightarrow F_N + 10\sin20^\circ &=& mg \\ \Rightarrow F_N &=& mg - 10\sin 20^\circ \\ &=& (2)(9.8) - 10\sin 20^\circ = 19.6 - 3.42 \\ &=& 16.18N \end{eqnarray}$

Simulation - Normal Force (click to hide)

Drag on the ground to tilt.
Drag on the blue arrow (the applied force) to change, or click "Remove Applied Force" to remove.
The red arrow represnts the total force.

Try It Yourself (click to show)

Exercise - normal force and a pushing force 1

$2kg$ block is pushed by a

$10N$ force at

$50^\circ$ on a frictionless surface as shown. We wish the normal force on the block later. As a first step, please identify the magnitude of the vertical component of

$F_1$ .

You will need to identify a right angle triangle under the vector to decompose it into its components.

Solution

The vertical component is the opposite side to

$50^\circ$ , so we use the

$\sin$ function. We are going to use this in a force diagram so we will only need the magnitude (as stated in the question), which means we do not use the negative sign to track its downward direction.

$10 \cos 50^\circ$

$10 \sin 50^\circ$

$-10 \cos 50^\circ$

$-10 \sin 50^\circ$

Feedback will appear here.

Exercise - normal force and a pushing force 2

Continue from the last problem, find the normal force.

Select unit:

$s$

$m/s^2$

$kg$

$N$

Draw a force diagram with only the vertical forces. There is no vertical acceleration, so all vertical forces must cancel.

Solution

Draw only the vertical forces in a force diagram. Since the block has no vertical movement, the vertical acceleration

$a_y$ is zero. This means all the vertical forces must cancel out:

$\begin{eqnarray} F_{up} &=& F_{down} \\ \Rightarrow F_N &=& mg + 10\sin 50^\circ \\ &=& (2)(9.8) + 10\sin 50^\circ = 19.6 + 7.66 \\ &=& 27.26N \end{eqnarray}$

Feedback will appear here.

PHYS 170

Introduction

A Brief Video Introduction on Newton's Laws (click to show)

The First Law

Inertia and Mass

Mass vs Weight

Try It Yourself (click to show)

Exercise - weight on earth and on the moon

Exercise - plane at constant velocity

Solution

The Second Law

Try It Yourself (click to show)

Exercise - a single force on a mass

Solution

Exercise - two opposing forces on a mass

Solution

Exercise - forces in two dimensions 1

Solution

Exercise - forces in two dimensions 2

Exercise - forces in two dimensions 3

Solution

The Third Law

Video on the Third Laws (click to show)

Opposing Forces

Example - horizontal opposing forces

Solution

Example - a block pulled vertically by two opposing forces (upward aa)

Solution

Try It Yourself (click to show)

Exercise - a block pulled vertically by two opposing forces (downward aa) 2

Solution

Exercise - a block pulled vertically by two opposing forces (downward aa) 3

Solution

Exercise - a block pulled vertically by two opposing forces (zero aa) 4

Solution

Normal Force

Example - Einstein on an elevator 1

Solution

Try It Yourself (click to show)

Exercise - Einstein on an elevator (upward aa) 2

Solution

Exercise - Einstein on an elevator (upward aa) 3

Solution

Exercise - Einstein on an elevator (zero aa) 4

Solution

Exercise - Einstein on an elevator (almost free fall) 5

Solution

Multiple Forces

Example - normal force and a pulling force

Solution

Simulation - Normal Force (click to hide)

Try It Yourself (click to show)

Exercise - normal force and a pushing force 1

Solution

Exercise - normal force and a pushing force 2

Solution

Notations

Example - a block pulled vertically by two opposing forces (upward $a$ )

Exercise - a block pulled vertically by two opposing forces (downward $a$ ) 2

Exercise - a block pulled vertically by two opposing forces (downward $a$ ) 3

Exercise - a block pulled vertically by two opposing forces (zero $a$ ) 4

Exercise - Einstein on an elevator (upward $a$ ) 2

Exercise - Einstein on an elevator (upward $a$ ) 3

Exercise - Einstein on an elevator (zero $a$ ) 4