Projectile Motion
In this section we will focus on one particular type of two dimensional called "projectile motion". It is the motion of an object flying under free fall (i.e. under the influence of gravity only). You will encounter some other two dimensional motions (such as circular motion, oscillations) in later chapters.
During free fall, the only force is gravity, which acts vertically. On the other hand, there are no forces in the horizontal direction (we ignore fiction and air resistance). As a result the acceleration along the horizontal and the vertical directions are not the same, and are given by (pay close attention to the minus sign in front of \(g\), indicating the vertical acceleration is downward): $$ \begin{eqnarray} a_x &=& 0 \\ a_y &=& - g = -9.8m/s^2 \end{eqnarray} $$ Remember \(g = 9.8m/s^2 \), not \(- 9.8m/s^2 \). If you mistakenly put in a negative value for \(g\), your \(a_y\) will have the wrong sign (and hence points up instead of down).
Furthermore, we will use the following convention: $$ \begin{eqnarray} s_{0x} &=& 0 \\ s_{0y} &=& 0 \end{eqnarray} $$ which amounts to setting the origin of the coordinate system to be at the initial postion of the object. In other words, it does not matter whether the projectile started from the ground, on the top of a cliff, in the greatest depth of a cave, in this convention we will always set the initial position to be the origin. Above the it \(s_y >0\), and below it \(s_y<0\).
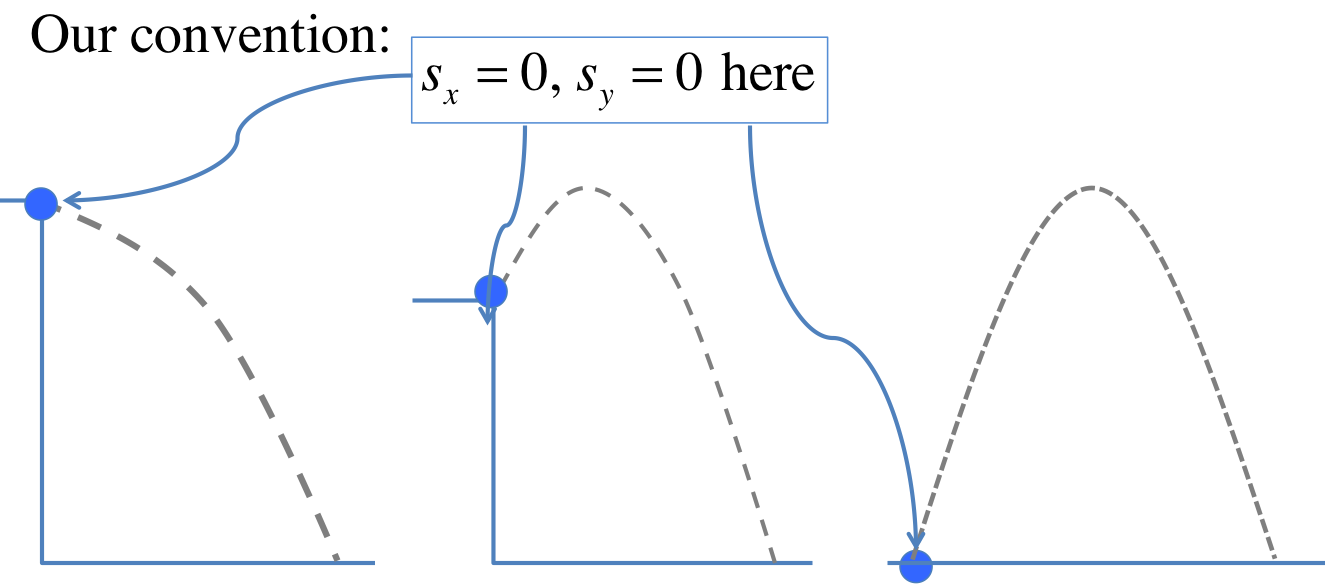
Putting all these assumptions (\(a_x=0, a_y=-g, s_{0x}=s_{0y}=0\)) into the two-dimensional equations from the last section, we get:
| \(x\) direction | \(y\) direction |
|---|---|
| \(s_x = v_{0x} t \) | \(s_y = v_{0y} t - \frac{1}{2} g t^2\) |
| \(v_x = v_{0x} \) | \(v_y = v_{0y} -g t \) |
These two equations will be sufficient in solving all the problems on projectile motion you encounter in this chapter.
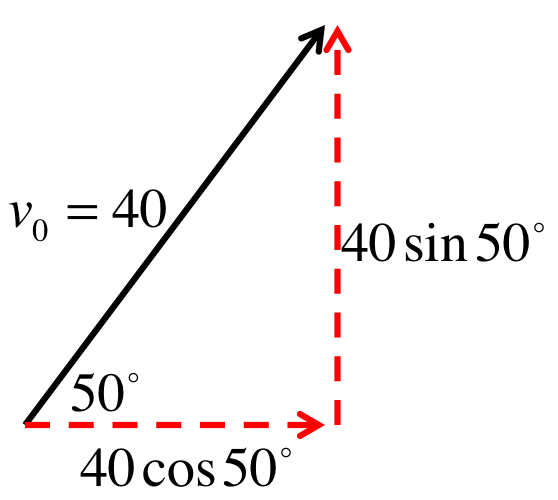
First we have to decompose the initial velocity into its \(x\) and \(y\) components because the two directions will evolve separately as if they are 2 one-dimensional problems.
From the figure of the left, one can read off the components: $$ \begin{eqnarray} v_{0x}&=& 40 \cos 50^\circ = 25.71m/s \\ v_{0y}&=& 40 \sin 50^\circ = 30.64m/s \end{eqnarray} $$
Finding the position means finding \(s_x\) and \(s_y\), so we can use the equations for projectile motion we find earlier, namely: $$ \begin{eqnarray} s_x&=& v_{0x} t\\ s_y &=& v_{0y}t - \frac{1}{2} g t^2 \end{eqnarray} $$ Knowing \(v_{0x}, v_{0y}\), and \(t=2s\), just substitute everything into the equations above to get: $$ \begin{eqnarray} s_x&=& v_{0x} t = (25.71)(2) = 51.42m\\ s_y &=& v_{0y}t - \frac{1}{2} g t^2 = (30.64)(2) - \frac{1}{2} (9.8)(2^2) = 41.68m \end{eqnarray} $$
"Height" obviously means \(s_y\). However, looking at the equation \(s_y = v_{0y}t - \frac{1}{2} g t^2\), which depends on \(t\), tells us we will need the time \(t_{top}\) when the ball reaches the maximum height.
Before trying to write down any equations, you must ask yourself: what do we know about the maximum point? What is the special characteristic of that point that will allow us to find the time?
The key point is this: \(v_y=0\) at the top.
The vertical velocity is changing direction at that point, switching from "up" (positive \(v_y\)) to "down" (negative \(v_y\)). Therefore at the turning point, its value must pass through 0. This gives: $$ \begin{eqnarray} 0&=& v_{y} = v_{0y} - g t_{top}\\ \Rightarrow t_{top}&=& \frac{v_{0y}}{g} = \frac{30.64}{9.8} = 3.13s \end{eqnarray} $$
Putting the time into the equation of \(s_y\), we get: $$ \begin{eqnarray} s_y &=& v_{0y} t_{top} -\frac{1}{2} g t_{top}^2 \\ &=& (30.64)(3.13) -\frac{1}{2} (9.8) (3.13^2) = 47.90m \end{eqnarray} $$
The horizontal range \(R\) is really the horizontal displacement \(s_x\), but its equation again depends on \(t\), so we will need to first figure out when the ball hits the ground. Similar to the last part, we have to ask, what is the special characteristic of the point of impact on the ground?
The key point is this: \(s_y=0\) when the ball hits the ground.
This makes sense because in getting the projectile equations we chose to put \(s_{0x} = s_{0y} = 0\) (therefore setting the orgin to be at the starting point), so when the ball comes back to the ground, the height \(s_y\) will become 0 once again. This gives: $$ \begin{eqnarray} 0&=& s_y = v_{0y}t - \frac{1}{2} g t^2 \\ \Rightarrow t(v_{0y} - \frac{1}{2} g t) &=& 0 \\ \Rightarrow v_{0y} - \frac{1}{2} g t &=& 0 \text{ or } t = 0 \text{ (rejected)}\\ \Rightarrow t_{ground} &=& \frac{2 v_{0y}}{g} = \frac{2 (30.64)}{9.8} = 6.25s \end{eqnarray} $$
Putting the time \(t_{ground}\) into \(s_x\) then gives the range \(R\): $$ \begin{eqnarray} R &=& s_x = v_{0x} t_{ground} \\ &=& (25.71)(6.25) = 160.77m \end{eqnarray} $$
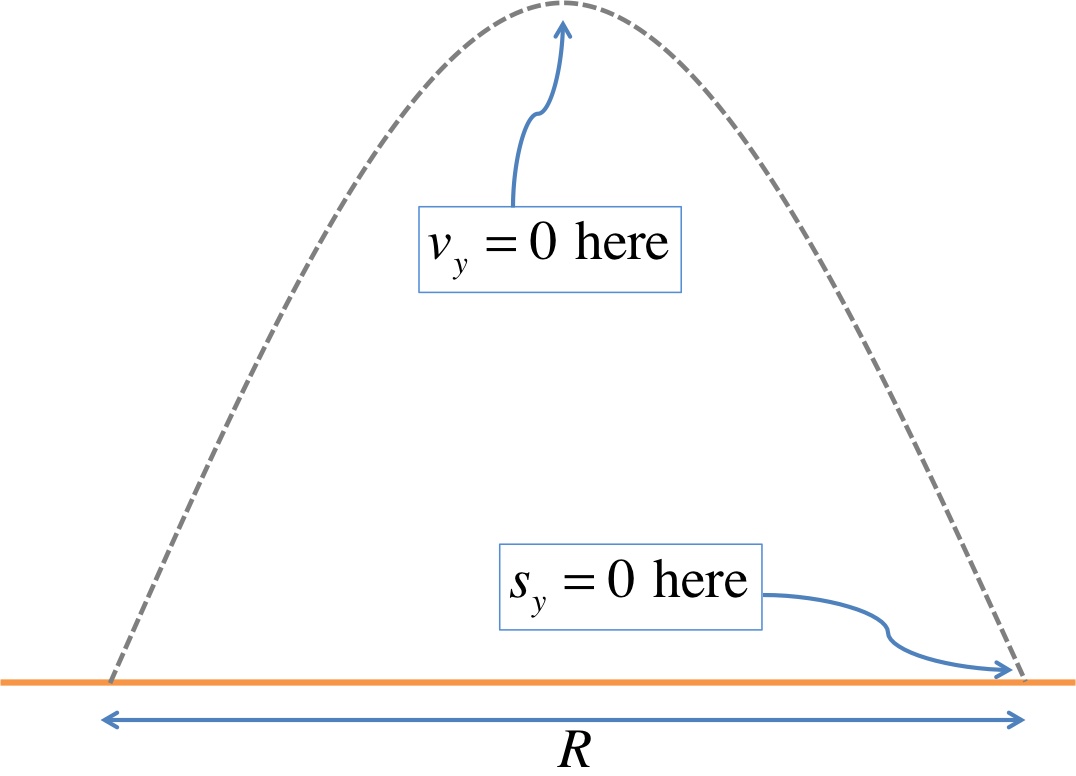
The key in solving the last two problems is in identifying the special characteristics of the points specified:
- At the top: \(v_y = 0\)
- At the ground level: \(s_y = 0\)
Try It Yourself (click to show)
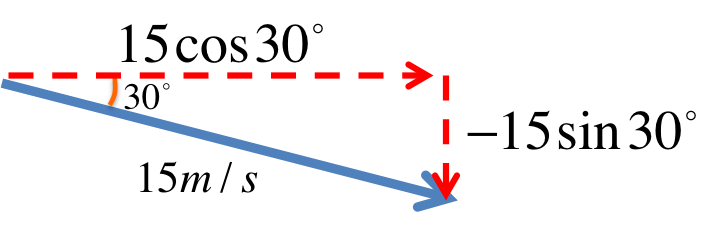
From the last problem, we learned that \(s_y=-50m\) at the bottom. Now we will substitute this into the equation of \(s_y\): $$ \begin{eqnarray} s_y &=& v_{0y} t - \frac{1}{2} g t^2 \\ \Rightarrow \frac{1}{2} g t^2 - v_{0y} t + s_y &=& 0 \\ \Rightarrow 4.9 t^2 + 7.5 t - 50 &=& 0 \end{eqnarray} $$
Because of the \(s_y \) term, it is not possible to factorize \(t\) out directly (unlike what we did in Projectile on a Flat Surface 4), we will use the quadratic formula: $$ \begin{eqnarray} t&=& \frac{-7.5 \pm \sqrt{7.5^2 - 4(4.9)(-50)}}{2(4.9)}\\ t &=& 2.52s \text{ or } t = -4.05s \text{ (rejected)} \end{eqnarray} $$
