PHYS 170

Three main variables to describe motion:

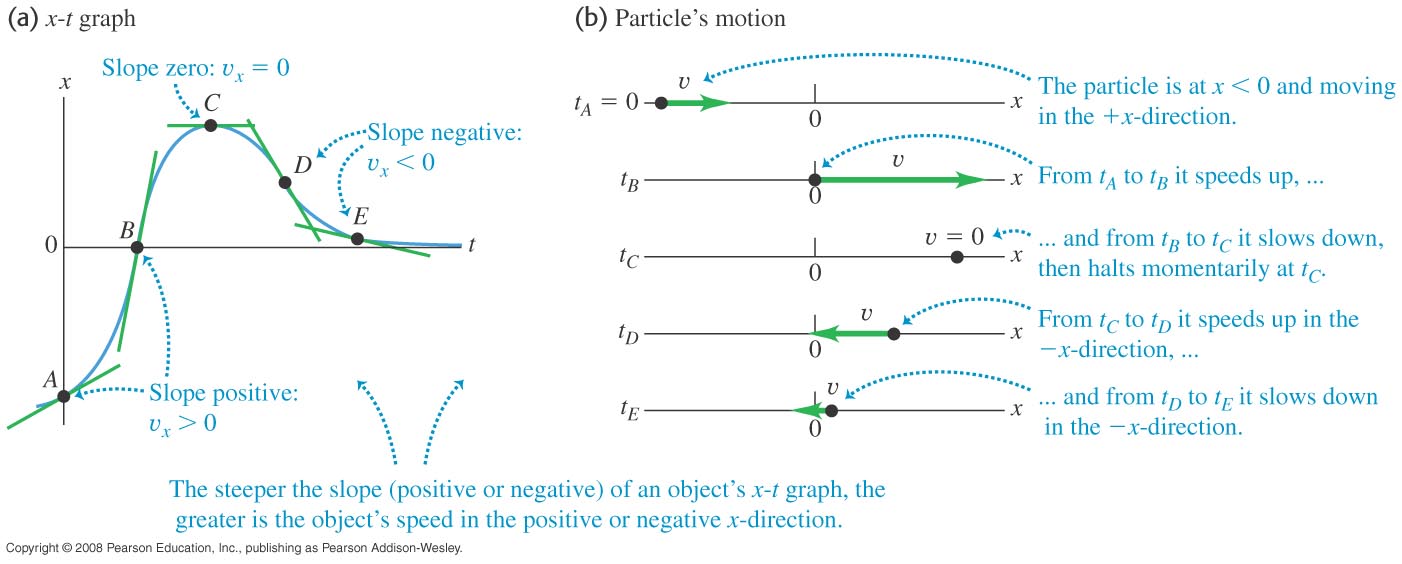
This chapter is about one dimensional motion only, so we do not need the full mathematics of vectors yet. Instead of writing \(\vec{s} = (-5\hat i)m\) for an object \(5m\) West of you, we will simply denote the direction using the sign as \(s=-5m\). In other words, in one dimension, there is no need to put the vector symbol (the little arrow) on the variables, and no need to use \(\hat i, \hat j\). Vectors will become useful in two or higher dimensions.

Sometimes \(s\) is denoted as \( x\) for horizontal motion, or \(y\) for vertical motion.

In calculus, "rate of change" literally means taking the time derivative (\(\frac{d}{dt}\)). Therefore: $$ \begin{eqnarray} v &=& \frac{ds}{dt} \\ a &=& \frac{dv}{dt} = \frac{d}{dt} (\frac{ds}{dt} ) = \frac{d^2s}{dt^2} \end{eqnarray} $$

One can have a rough idea about the meanings using the following approximation: $$ \begin{eqnarray} v &=& \frac{ds}{dt} &\approx& \frac{\Delta s}{\Delta t} = \frac{\text{change in displacement}}{\text{change in time}} \\ a &=& \frac{dv}{dt} &\approx& \frac{\Delta v}{\Delta t} = \frac{\text{change in velocity}}{\text{change in time}} \end{eqnarray} $$ where the symbol \(\Delta\) means "change". It is always computed by final value minus the initial value, like so: $$ \Delta s = s_{final} - s_{initial} \\ \Delta v = v_{final} - v_{initial} $$

Velocity vs Speed

In physics the word "speed" is not the same as "velocity". Speed means the magnitude of velocity, i.e. speed = \(|\vec{v}|\). For example, say you calculate \(v=-3m/s\) in a 1D problem (negative because the object is moving left), if the question asks you for the "speed", you must answer \(3m/s\) instead of \(-3m/s\). If your online homework said you had the wrong sign in an answer even though you followed the sign convention correctly, read the question carefully, did it ask you for the velocity or the speed? Many students are not observant enough and it becomes a major source of confusion.

I will assume that you already know how to calculate the slope of a straight line, and that you know the following meanings:

• Positive slope: line going up
• Zero slope: line staying the same height
• Negative slope: line going down

There are multiple ways to calculate the slope, but in our application here the fastest way is the method "Rise over Run": $$ slope = \frac{rise}{run} = \frac{\Delta y}{\Delta x} $$ where "rise" stands for the vertical change, and "run" stands for the horizontal change. Below are two videos that refeshes your memory, in particular, you will need to be able to handle negative slope, so pay some attention to the second video.

Slope in physics (unlike in your Math courses) almost always carries its own unit, and is given by: $$ \text{unit of the slope} = \frac{\text{unit of the y-axis}}{\text{unit of the x-axis}} $$ For example, if the y-axis is displacement measured in \(m\) while the x-axis is time measured in \(s\), then the unit of the slope will be \(m/s\). If the y-axis is in \(m/s\), the x-axis is in \(s\), then the slope will be in \(m/s^2\).

Try It Yourself (click to show)

We will learn how to analyze three types of graphs that describe motion, they are:

• \(st\) graph (displacement vs time graph)
• \(vt\) graph (velocity vs time graph)
• \(at\) graph (acceleration vs time graph)

Here is an \(st\) graph (displacement \(s\) is denoted as \(x\)) and an explanation of the motion it represents:

Since the y-axis is the horizontal displacement \(x\), one could obviously read off the position \(x\) from the graph. Less obvious, is that you could also read off the velocity by calculating the slope of the graph as you could see in the figure above. Here is the rule concerning slopes of such motion graphs:

Try It Yourself (click to show)

As you saw before, slope allows you to start from \(s\) to \(v\) to \(t\). It turns out the area of the graph allows you to go from \(a\) to \(v\) to \(s\):

Try It Yourself (click to show)

Try It Yourself (click to show)