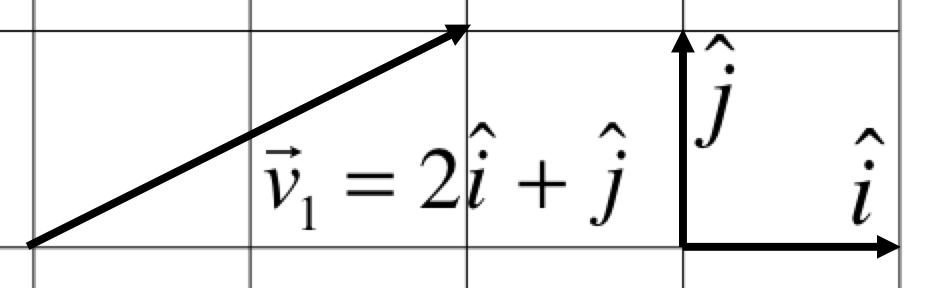Lecture 01 - Vectors

Introduction

Here is a simple picture of two vectors:

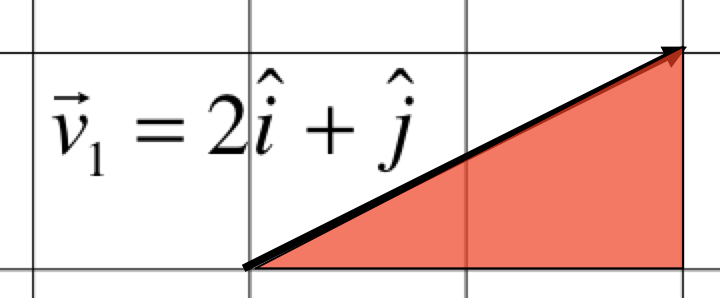
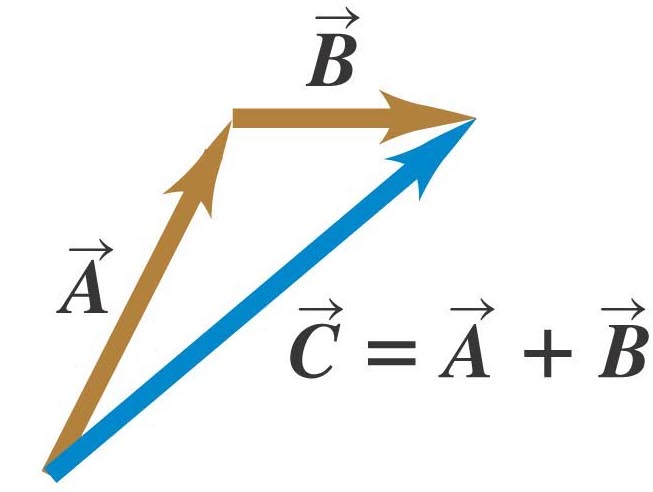
A vector is a straight arrow. It carries two pieces of information:

Magnitude (length of the arrow)
Direction (angle with the positive $ x $-axis)

Examples of vectors:

force (you could push in different directions with different strength)
velocity (a bird could fly in different direction fast or slow)
displacement (which direction you move and how far you move)

A vector is denoted in calcuations with a tiny arrow on the top. For example, a vector named "$ v $" is denoted as $ \vec{v} $.

The arrow on the top of $v$ is not optional, you will be penalized in the exams omitting it.

In mathematics, a quantity that is just a number (without direction) is called a scalar. You can think of scalar as the "opposite" of vector. Temperature is an example of a scalar. If you say today's temperature is $25^\circ C$, no direction is needed, so we write temperature as $T$ and not $\vec{T}$. Other examples of scalars are energy ($E$), work ($W$), mass ($m$), and many more. We do not put the little arrow on the top of a scalar.

Vector Components

We now learn how to represent a vector mathematically (it is too much trouble drawing the picture of an arrow everytime!). Imagine you want to tell someone to walk in the following direction:

3 meters East, 4 meters North

You can describe the walk by the vector:
$$ \vec{v} = ( 3\hat i + 4 \hat j ) m$$

Likewise, you could translate "5 meters West, 6 meters South" as the following:
$$ \vec{v} = ( -5 \hat i -6 \hat j ) m$$

You could probably guess the following: $$ \begin{align} \text{East} &\rightarrow +\hat i \\ \text{West} &\rightarrow -\hat i \\ \text{North} &\rightarrow +\hat j \\ \text{South} &\rightarrow -\hat j \end{align} $$ For simplicity, we will ignore the unit (the "$ m $" for meters above) of the vector below. You will see later that a vector could take on different units depending on what it represents.

The x and y Components

Take the vector $ \vec{v} = -5 \hat i -6 \hat j $, we call -5 and -6 the x and y components of $\vec{v} $. The components are denoted as: $$ v_x = -5 \\ v_y = -6 $$ Note that there are no $\hat i, \hat j $ on the right hand side. This means that $ v_x $ and $ v_y$ are just numbers as opposed to vectors, therefore there are no little "arrow" above the $ v_x $ and $ v_y$.

Simulation - Vector Components (click to hide)

Drag the head of the arrow to see how its components change.

Question will be loaded by load_exercise_example_all() defined in script_question.js

Try It Yourself (click to show)

Question will be loaded by load_exercise_example_all() defined in script_question.js

Magnitude

Magnitude simply means "the length of a vector". Take a look at the vector $ \vec{v_1} $ below:

How long is the vector?

If you could imagine a triangle below the vector, you will realize the length of the vector is simply the hypotenuse of the triangle.

magnitude of vector by Pythagoras's theorem

You can now figure out the magnitude using the Pythagoras's theorem: $$ |\vec{v_1}| = \sqrt{2^2 + 1^2} = \sqrt{5} \approx 2.24 $$

Question will be loaded by load_exercise_example_all() defined in script_question.js

Try It Yourself (click to show)

Question will be loaded by load_exercise_example_all() defined in script_question.js

Addition and Subtraction of Vectors

Vectors can be added or subtracted "component by component". For example:
$$ \left\{ \begin{array}{l} \vec{u} = 10 \hat i + 7 \hat j \\ \vec{v} = 3 \hat i -2 \hat j \end{array} \right. \Rightarrow \left\{ \begin{array}{l} \vec{u} + \vec{v}= 13 \hat i + 5 \hat j \\ \vec{u} - \vec{v} = 7 \hat i +9 \hat j \end{array} \right. $$

This allows us to calculate things like $ |\vec{u} - \vec{v}| $: $$ |\vec{u} - \vec{v}| = |7 \hat i +9 \hat j| = \sqrt{7^2 + 9^2} = 11.40 $$

Vectors addition also has a geometrical meaning as you could see in the figure below. You can think of $ \vec{A} + \vec{B} $ as someone first walking in the $ \vec{A} $ direction then in the $ \vec{B} $ direction. You can see that vectors can be added geometrically by placing them head to tail.

Simulation - Vector Addition (click to hide)

Drag vectors out of the box, drag back to remove.
The individual vectors can be changed by dragging.
The red arrow is the sum of all the vectors.

Activity

Drag to line up (tail of one arrow on the head of another) all the blue arrows to see if they always combine to give the red arrow.
Line them up in a different order to see if they still produce the same total (red) vector.
Write out each vector in component form (i.e. with $\hat i$ and $\hat j$) and add them up algebraically to see if it gives the same result.

One could also multiple or divide a number to a vector. For example: $$ \begin{eqnarray} 2\vec{v} &=& 2( 3 \hat i -2 \hat j) = 6 \hat i -4 \hat j \\ -\vec{v} &=& -( 3 \hat i -2 \hat j) = -3 \hat i +2 \hat j \\ \frac{1}{2}\vec{v} &=& \frac{1}{2} ( 3 \hat i -2 \hat j) = 1.5 \hat i - \hat j \end{eqnarray} $$ Multiplying $\vec{v}$ by 2 makes it twice as long, multiplying -1 reverses its direction, while dividing by 2 makes it half as long.

Try It Yourself (click to show)

Question will be loaded by load_exercise_example_all() defined in script_question.js

Decomposing a Vector

It is assumed that you have some basic knowledge of trigonometry. If you are new to trigonometry, click here for the bare essentials.

"Decomposing a vector" means finding the x and y components of a vector. Usually you will need to use some trignometry to get the answer.

Question will be loaded by load_exercise_example_all() defined in script_question.js

Simulation - Vector Decomposition (click to hide)

Drag the head of the arrow to see how its components change.
Click "Switch View" to see different way to visualize the decomposition.

Try It Yourself (click to show)

Question will be loaded by load_exercise_example_all() defined in script_question.js

Video on Decomposing Vectors (click to show)

The Angle of a Vector

It is assumed that you have some basic knowledge of trigonometry. If you are new to trigonometry, click here for the bare essentials.

Unless any other axes are specified, when you are asked to find "the angle of a vector", it means the angle the vector makes with the positive x-axis. The basic formula for find the the angle of a vector $\vec{v} = a \hat i + b\hat j$ is:

$$ \theta = \tan^{-1} (\frac{b}{a}) + \phi $$

where $\phi= 0^\circ$ if $a>0$, and $\phi= 180^\circ$ if $a<0$.
In other words, the $tan^{-1}$ function only gives the right answer when the x-component is positive. Whenever the x-component is negative, you have to add $180^\circ$ to the result of the $tan^{-1}$ function.

Question will be loaded by load_exercise_example_all() defined in script_question.js

Check out the angle calculations below the simulation earlier (click here).

Try It Yourself (click to show)

Question will be loaded by load_exercise_example_all() defined in script_question.js

Units

In Physics (as opposed to in your Math classes), vectors almost always have units. While we have been ignoring the units for simplicity earlier, you should remember to include them in the exams. A vector $\vec{s}$ that describes position (what physicists call "displacement") in meters, we would write as: $$ \vec{s} = (3\hat i - 4\hat j) m $$ Note that the unit "$m$" is written outside the parenthese.

If a vector $\vec{v}$ is describing velocity in $m/s$ (meters per second), then we write: $$ \vec{v} = (-23\hat i - 7\hat j) m/s $$

Other common vectors you will meet later are acceleration and force (units are "meters per second squared" and "Newtons"). $$ \vec{a} = (-23\hat i - 7\hat j) m/s^2 \\ \vec{F} = (-23\hat i - 7\hat j) N $$

PHYS 170

Introduction

Vector Components

The x and y Components

Simulation - Vector Components (click to hide)

Try It Yourself (click to show)

Magnitude

Try It Yourself (click to show)

Addition and Subtraction of Vectors

Simulation - Vector Addition (click to hide)

Activity

Try It Yourself (click to show)

Decomposing a Vector

Simulation - Vector Decomposition (click to hide)

Try It Yourself (click to show)

Video on Decomposing Vectors (click to show)

The Angle of a Vector

Try It Yourself (click to show)

Units

Notations