thermodynamics || thermodynamics_second || entropy
Exercise - entropy with no change in temperature $\Delta T = 0$
A very large object is at $200K$. It is so large that any changes in temperature can be ignored.
In case 1, it gains $1000J$ of heat, what is its change of entropy $\Delta S_1$?
In case 2, the same object loses $800J$ of heat, what is the change in entropy $\Delta S_2$?
If $\Delta T = 0$, use $\Delta S = \frac{Q}{T}$. However, watch out for the sign of $Q$.
Recall that $Q\gt 0$ when an object gains heat, and $Q\lt 0$ when it loses heat.
Solution
Recall that $Q\gt 0$ when an object gains heat, and $Q\lt 0$ when it loses heat, so for case 1 $Q_1 = +1000J$, and for case 2 $Q_2 = -800J$. Since $\Delta T = 0$, we can use $\Delta S = \frac{Q}{T}$ to do both cases.
$$
\begin{eqnarray}
\Delta S_1 &=& \frac{+1000J}{200K} \\
&=& + 5J/K\\
\Delta S_2 &=& \frac{-800J}{200K} \\
&=& -4 J/K
\end{eqnarray}
$$
Generally when an object loses heat its entropy decreases, hence the negative change in entropy in case 2.
$\Delta S_1 = $
5
0
$\Delta S_2 = $
-4
0
Select unit:
$J$
$K$
$J/K$
$K/J$
2
Feedback will appear here.
thermodynamics || thermodynamics_second || entropy
Exercise - entropy during heat exchange
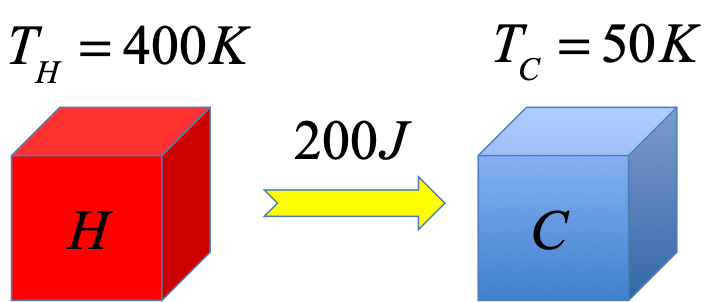
$200J$ of heat is transferred from an hot object "$H$" at $T_H=400K$ to a cold object "$C$" at $T_C=50K$? Calculate the change in entropy of each of the objects and also the total change in entropy for the whole system. Assume both objects are large enough that temperature change could be neglected.
If $\Delta T = 0$, then use $\Delta S = \frac{Q}{T}$. Be careful with the sign of $Q$.
$Q_H\lt 0$ for $H$ but $Q_C \gt 0$ for $C$.
Solution
Because $\Delta T = 0$, then use $\Delta S = \frac{Q}{T}$. Since $H$ is losing heat, $Q_H = -200J$. $C$ is gaining heat, so $Q_C = +200J$.
$$
\begin{eqnarray}
\Delta S_H &=& \frac{Q_H}{T} \\
&=& \frac{-200J}{400K} \\
&=& -0.5J/K \\
\Delta S_C &=& \frac{Q_C}{T} \\
&=& \frac{+200J}{50K} \\
&=& +4 J/K \\
\Rightarrow \Delta S_{total} &=& \Delta S_H + \Delta S_C = -0.5 + 4 = 3.5J/K
\end{eqnarray}
$$
$\Delta S_H = $
-0.5
0.1
$\Delta S_C = $
4
0.1
$\Delta S_{total} = $
3.5
0.2
Select unit:
$N$
$J$
$K$
$J/K$
3
Feedback will appear here.
thermodynamics || thermodynamics_second || entropy || specific_heat
Exercise - entropy with change in temperature $\Delta T \neq 0$
A $4kg$ object with $c=500JK^{-1}kg^{-1}$ is at $200K$.
In case 1, its temperature is increased to $300K$, what is its change of entropy $\Delta S_1$?
In case 2, the temperature is decreased to $100K$, what is the change in entropy $\Delta S_2$?
If $\Delta T \neq 0$, use $\Delta S = mc \ln\frac{T_f}{T_i}$.
Solution
$$
\begin{eqnarray}
\Delta S_1 &=& mc \ln\frac{T_f}{T_i} \\
&=& (4kg)(500JK^{-1}kg^{-1}) \ln\frac{300}{200} \\
&=& 810.93J/K \\
\Delta S_2 &=& &=& mc \ln\frac{T_f}{T_i} \\
&=& (4kg)(500JK^{-1}kg^{-1}) \ln\frac{100}{200} \\
&=& -1386.29J/K
\end{eqnarray}
$$
Generally when an object loses heat its entropy decreases, hence the negative change in entropy in case 2.
$\Delta S_1 = $
810.93
50
$\Delta S_2 = $
-1386.29
50
Select unit:
$J$
$K$
$J/K$
$K/J$
2
Feedback will appear here.
thermodynamics || thermodynamics_second || entropy || latent_heat
Exercise - entropy with change of phase
A $5kg$ sample is known to have a melting point of $-50^\circ C$ and a boiling point of $240^\circ C$. Its latent heat of fusion is $64kJ/kg$ and its latent heat of vaporization is $200kJ/kg$.
In case 1, the sample in liquid form is vaporized at its boiling point, what is its change of entropy $\Delta S_1$?
In case 2, the sample in liquid form is frozen at its melting point, what is the change in entropy $\Delta S_2$?
If $\Delta T = 0$, use $\Delta S = \frac{Q}{T}$. However, watch out for the sign of $Q = \pm mL$.
Recall that $Q\gt 0$ when an object gains heat, and $Q\lt 0$ when it loses heat, so choose the sign of $Q = \pm mL$ carefully.
Solution
Recall that $Q\gt 0$ when an object gains heat, and $Q\lt 0$ when it loses heat, so for case 1 $Q_1 = +mL_v$, and for case 2 $Q_2 = -mL_f$. Since $\Delta T = 0$, we can use $\Delta S = \frac{Q}{T}$ to do both cases.
$$
\begin{eqnarray}
\Delta S_1 &=& \frac{+mL_v}{T_{boiling}} \\
&=& \frac{+(5kg)(200kJ/kg)}{(240+273)K} \\
&=& + 1949.32 J/K\\
\Delta S_2 &=& \frac{-mL_f}{T_{melting}} \\
&=& \frac{-(5kg)(64kJ/kg)}{(-50+273)K} \\
&=& -1434.98 J/K\\
\end{eqnarray}
$$
Generally when an object loses heat its entropy decreases, hence the negative change in entropy in case 2.
$\Delta S_1 = $
1949.32
100
$\Delta S_2 = $
-1434.98
100
Select unit:
$J$
$K$
$J/K$
$K/J$
2
Feedback will appear here.
thermodynamics || thermodynamics_second || entropy || latent_heat
Example - entropy of ice to steam 1
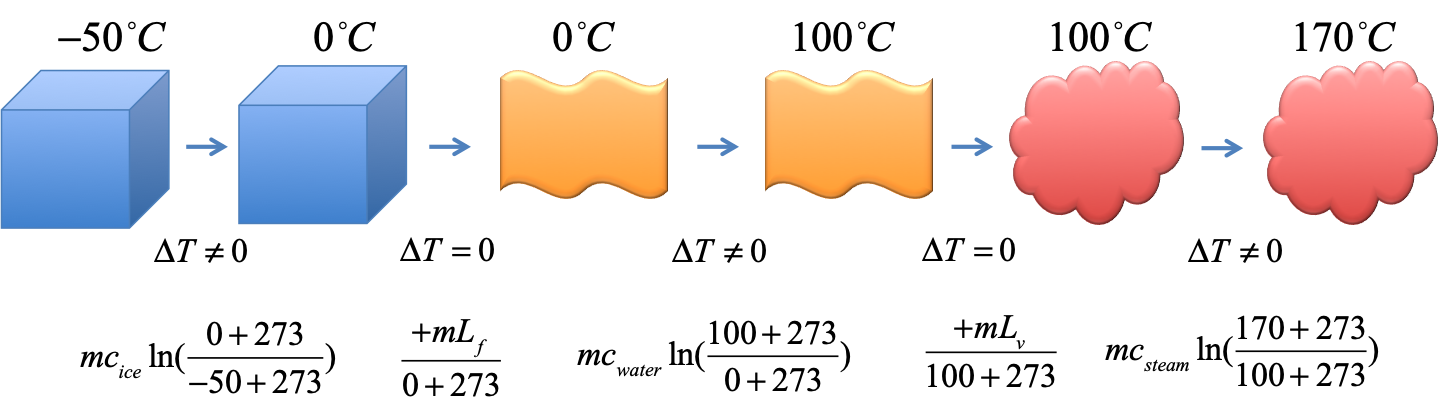
$3kg$ of ice at $-50^\circ C$ is heated into steam at $170^\circ C$. Find the total change in entropy in the process.
Use $c_{ice} = 2090JK^{-1}kg^{-1}$, $c_{water}=4186JK^{-1}kg^{-1}$, $c_{steam}=1930JK^{-1}kg^{-1}$, $L_f =334kJ/kg$, $L_v = 2254kJ/kg$. Pay attention to the units of $c$ and $L$ ($J$ vs $kJ$).
Solution
$$
\begin{eqnarray}
\Delta S_1 &=& mc_{ice}\ln(\frac{0+273}{-50+273}) &= (3kg)(2090JK^{-1}kg^{-1})\ln(\frac{273}{223}) &= 1268.42J/K \\
\Delta S_2 &=& \frac{mL_f}{0+273} &= \frac{(3kg)(334kJ/kg)}{273K} &= 3670.32J/K\\
\Delta S_3 &=& mc_{water}\ln(\frac{100+273}{0+273}) &= (3kg)(4186JK^{-1}kg^{-1})\ln(\frac{373}{273}) &= 3919.43J/K \\
\Delta S_4 &=& \frac{mL_v}{100+273} &= \frac{(3kg)(2254kJ/kg)}{373K} &= 18128.69J/K\\
\Delta S_5 &=& mc_{steam}\ln(\frac{170+273}{100+273}) &= (3kg)(1930JK^{-1}kg^{-1})\ln(\frac{443}{373}) &= 995.83J/K \\
\Rightarrow \Delta S_{total} &=& 27982.69J/K &= 27.98 kJ/K&
\end{eqnarray}
$$
Note the units of $c$ and $L$ are slightly different ($J$ vs $kJ$) and see how they work out in $kJ/K$.
thermodynamics || thermodynamics_second || entropy || latent_heat
Exercise - entropy of ice to steam 2
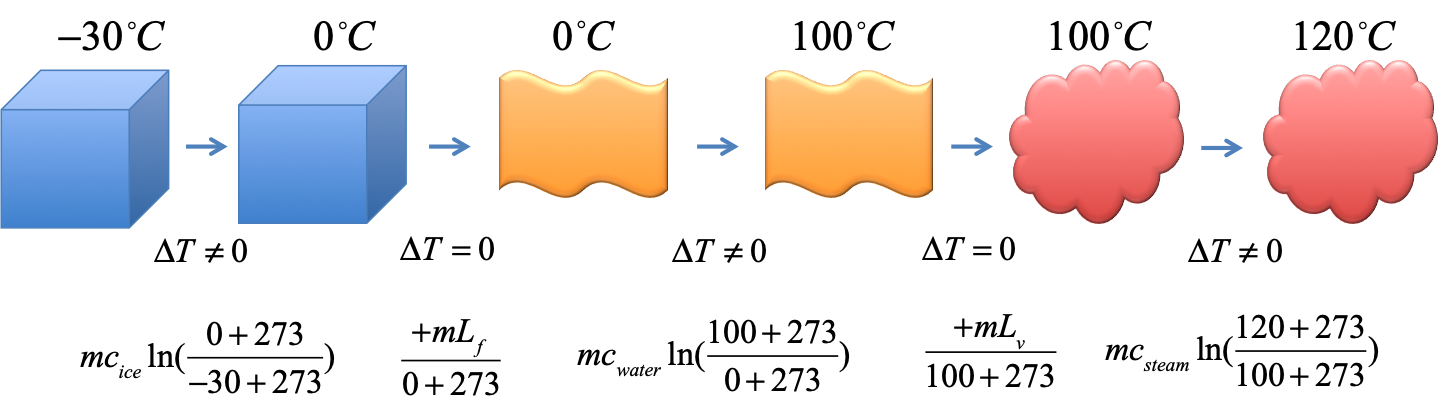
$3kg$ of ice at $-30^\circ C$ is heated into steam at $120^\circ C$. Find the total change in entropy in the process.
Use $c_{ice} = 2090JK^{-1}kg^{-1}$, $c_{water}=4186JK^{-1}kg^{-1}$, $c_{steam}=1930JK^{-1}kg^{-1}$, $L_f =334kJ/kg$, $L_v = 2254kJ/kg$. Pay attention to the units of $c$ and $L$ ($J$ vs $kJ$).
Solution
$$
\begin{eqnarray}
\Delta S_1 &=& mc_{ice}\ln(\frac{0+273}{-30+273}) &= (3kg)(2090JK^{-1}kg^{-1})\ln(\frac{273}{243}) &= 729.89J/K \\
\Delta S_2 &=& \frac{mL_f}{0+273} &= \frac{(3kg)(334kJ/kg)}{273K} &= 3670.32J/K\\
\Delta S_3 &=& mc_{water}\ln(\frac{100+273}{0+273}) &= (3kg)(4186JK^{-1}kg^{-1})\ln(\frac{373}{273}) &= 3919.43J/K \\
\Delta S_4 &=& \frac{mL_v}{100+273} &= \frac{(3kg)(2254kJ/kg)}{373K} &= 18128.69J/K\\
\Delta S_5 &=& mc_{steam}\ln(\frac{120+273}{100+273}) &= (3kg)(1930JK^{-1}kg^{-1})\ln(\frac{393}{373}) &= 302.42J/K \\
\Rightarrow \Delta S_{total} &=& 26750.75J/K &= 26.75 kJ/K&
\end{eqnarray}
$$
Note the units of $c$ and $L$ are slightly different ($J$ vs $kJ$) and see how they work out in $kJ/K$.
26.75
0.2
$kJ/K$
Feedback will appear here.
thermodynamics || thermodynamics_second || entropy || latent_heat
Exercise - entropy of water to ice
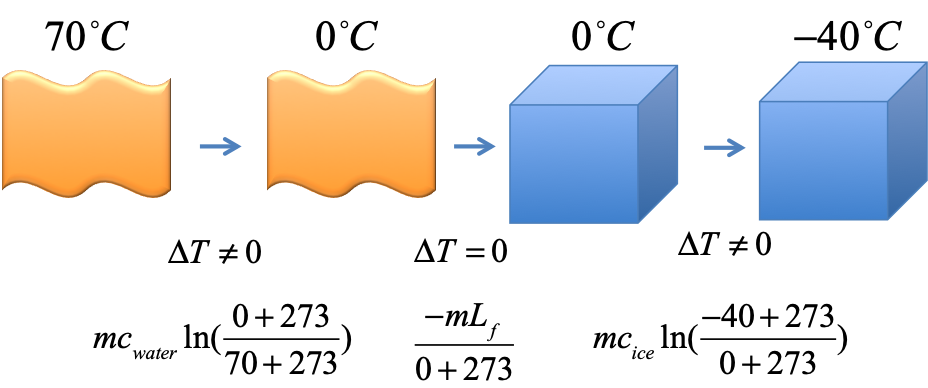
$5kg$ of water at $70^\circ C$ is frozen into ice at $-40^\circ C$. Find the total change in entropy in the process.
Use $c_{ice} = 2090JK^{-1}kg^{-1}$, $c_{water}=4186JK^{-1}kg^{-1}$, $c_{steam}=1930JK^{-1}kg^{-1}$, $L_f =334kJ/kg$, $L_v = 2254kJ/kg$. Pay attention to the units of $c$ and $L$ ($J$ vs $kJ$).
Solution
$$
\begin{eqnarray}
\Delta S_1 &=& mc_{water}\ln(\frac{0+273}{70+273}) &= (3kg)(4186JK^{-1}kg^{-1})\ln(\frac{273}{343}) &= -2866.47 J/K \\
\Delta S_2 &=& \frac{-mL_f}{0+273} &= \frac{-(3kg)(334kJ/kg)}{273} &= -3670.33 J/K\\
\Delta S_3 &=& mc_{ice}\ln(\frac{-40+273}{0+273}) &= (3kg)(2090JK^{-1}kg^{-1})\ln(\frac{233}{273}) &= -993.38 J/K \\
\Rightarrow \Delta S_{total} &=& -7530.18 J/K &&
\end{eqnarray}
$$
-7530.18
50
Select unit:
$J$
$K$
$J/K$
$K/J$
2
Feedback will appear here.
thermodynamics || thermodynamics_second || entropy || heat_engine
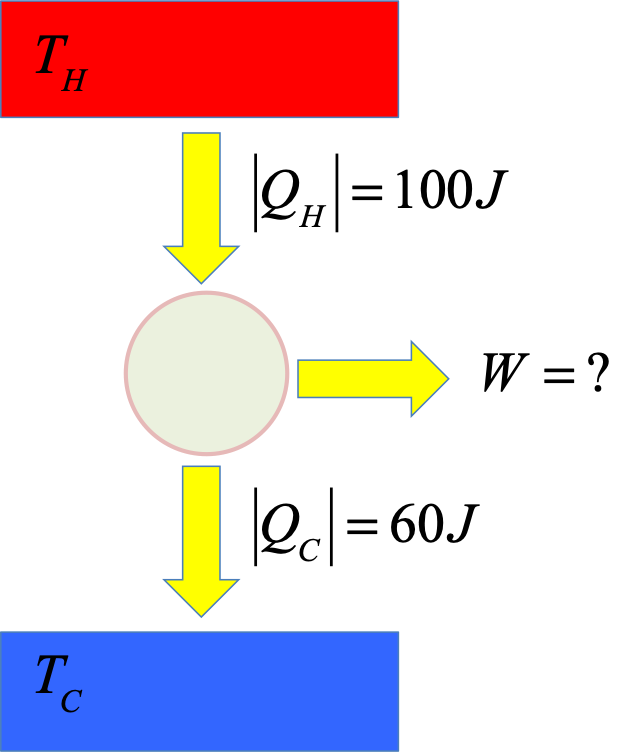
Exercise - heat engine 1
Find the useful work done by the engine and its efficiency.
Solution
By conservation of energy:
$$
\begin{eqnarray}
W &=& |Q_H| - |Q_C|\\
&=& 100J - 60J = 40J
\end{eqnarray}
$$
Put into the definition of the efficiency:
$$
e = \frac{W}{|Q_H|} = \frac{40}{100} = 40\%
$$
$W=$
40
0
$J$
$e = $
40
0
$\%$
Feedback will appear here.
thermodynamics || thermodynamics_second || entropy || heat_engine
Exercise - heat engine 2
An engine has an efficiency of $80\%$. Given the engine produces useful work of $100J$, find $|Q_H|$ and $|Q_C|$.
Solution
By the definition of efficiency:
$$
\begin{eqnarray}
e &=& \frac{W}{|Q_H|} \\
\Rightarrow |Q_H| &=& \frac{W}{e} \\
&=& \frac{100J}{0.8} \\
&=& 125J
\end{eqnarray}
$$
By conservation of energy:
$$
\begin{eqnarray}
|Q_H| &=& W + |Q_C|\\
\Rightarrow |Q_C| &=& |Q_H| - W \\
&=& 125J - 100J = 25J
\end{eqnarray}
$$
$|Q_H|=$
125
2
$|Q_C|=$
25
2
Select unit:
$J$
$N$
$W$
$K$
0
Feedback will appear here.
thermodynamics || thermodynamics_second || entropy || heat_engine
Exercise - reversible heat engine 1
Given $T_H = 600K$, $T_C=200K$ for a reversible engine, if the engine releases $50J$ of heat to the environment for each cycle, find the heat input and the useful work the engine produces.
For a reversible engine, $\frac{T_C}{T_H} = \frac{|Q_C|}{|Q_H|} $, from which you could solve for $|Q_H|$.
Solution
It is given that $Q_C=50J$. Because it is a reversible engine, we have $\frac{T_C}{T_H} = \frac{|Q_C|}{|Q_H|} $.
$$
\begin{eqnarray}
\frac{T_C}{T_H} &=& \frac{|Q_C|}{|Q_H|} \\
\Rightarrow |Q_H| &=& \frac{T_H}{T_C} |Q_C| \\
&=& \frac{600}{200} (50J) \\
&=& 150J
\end{eqnarray}
$$
By conservation of energy, we have:
$$
\begin{eqnarray}
W &=& |Q_H| - |Q_C| \\
&=& 150J - 50J \\
&=& 100J
\end{eqnarray}
$$
$|Q_H| = $
150
2
$W = $
100
2
Select unit:
$J$
$N$
$W$
$K$
0
Feedback will appear here.
thermodynamics || thermodynamics_second || entropy || heat_engine
Exercise - reversible heat engine 2
A reversible engine has an efficency of $80\%$. Given $|Q_H|= 100J$ and $T_C = 200K$, find $W$, $|Q_C|$, and $T_H$.
For a reversible engine, $e =\frac{W}{|Q_H|} $, from which you could solve for $W$.
$W$ and $|Q_H|$ will give $|Q_C|$, and $\frac{|Q_C|}{|Q_H|} = \frac{T_C}{T_H}$ will give $T_H$.
Solution
$$
\begin{eqnarray}
e &=& \frac{W}{|Q_H|} \\
\Rightarrow W &=& e |Q_H| \\
&=& (0.8)(100J)\\
&=& 80 J
\end{eqnarray}
$$
By conservation of energy:
$$
\begin{eqnarray}
|Q_H| &=& W + |Q_C|\\
\Rightarrow |Q_C| &=& |Q_H| - W \\
&=& 100J - 80J \\
&=& 20J
\end{eqnarray}
$$
Because the engine is reversible:
$$
\begin{eqnarray}
\frac{T_H}{T_C} &=& \frac{|Q_H|}{|Q_C|} \\
T_H &=& \frac{|Q_H|}{|Q_C|} T_C \\
&=& \frac{100}{20} (200K) \\
&=& 1000K
\end{eqnarray}
$$
$W = $
80
2
$J$
$|Q_C| = $
20
2
$J$
$T_H = $
1000
50
$K$
Feedback will appear here.
