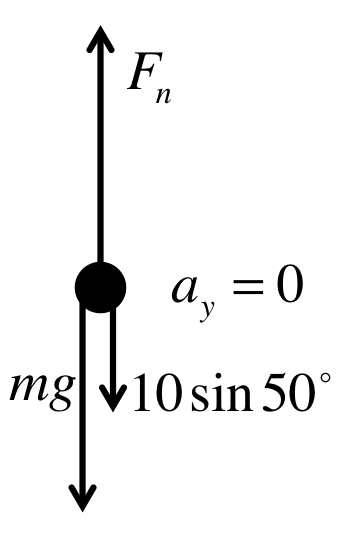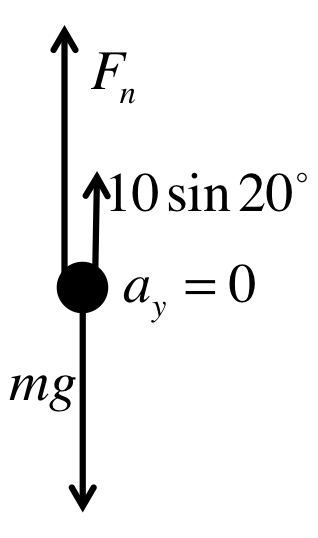force || incline
Example - pulling a block down a frictionless incline
A block $m = 2kg$ on a frictionless incline ($\theta = 30^\circ$) is being pulled down the slope with a tension force of $T=15N$. Find the accerlation and the normal force.
Solution
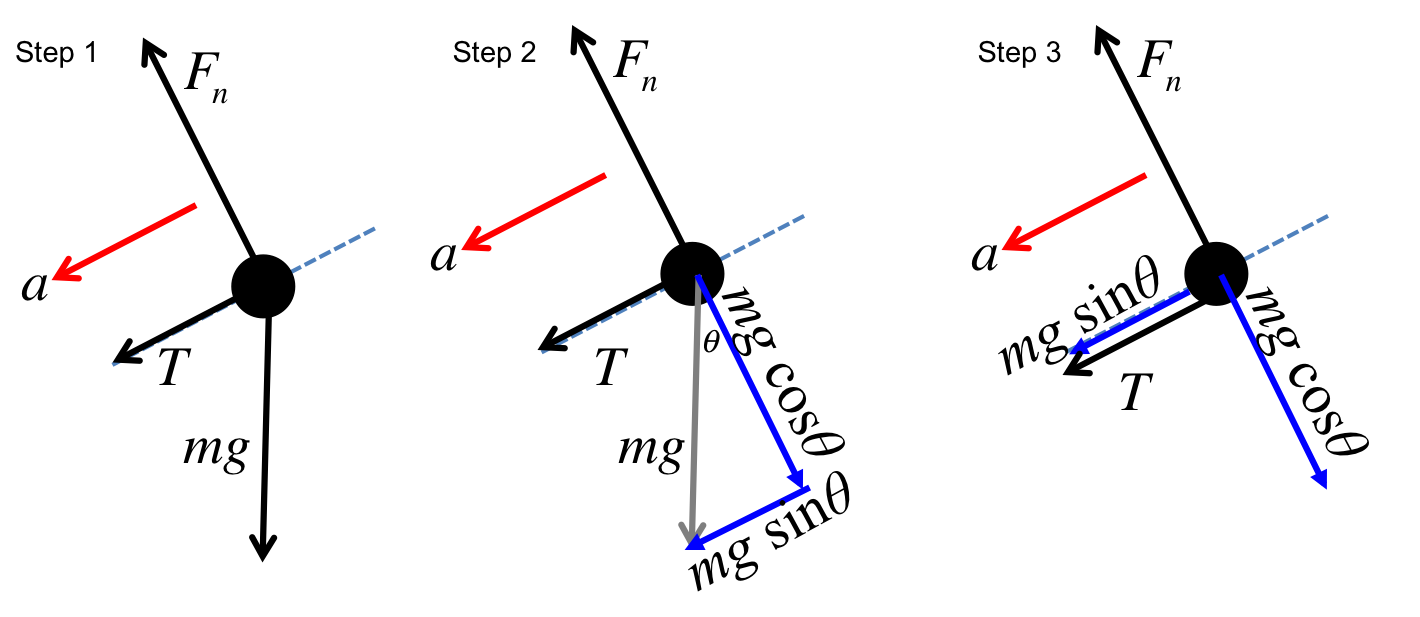
The force diagram is analysed just as before. The only difference is in the appearance of an additional force $T$. Along the parallel direction, however this is merely one more force to include in the net force:
$$
\begin{eqnarray}
mg\sin\theta + T &=& m a \\
\Rightarrow a &=& g\sin\theta + \frac{T}{m}\\
&=& 9.8\sin30^\circ + \frac{15}{2} \\
&=& 4.9 + 7.5 = 12.4m/s^2
\end{eqnarray}
$$
In the perpendicular direction, the tension has no effect. Again, using the fact that $a_\perp = 0$, we can conclude $F_n = mg\cos30^\circ = 16.97N$.
force || incline
Exercise - pulling a block up a frictionless incline 1
A block $m = 2kg$ on a frictionless incline ($\theta = 30^\circ$) is being pulled up the slope with a tension force of $T=15N$. To find the magnitude of the accerlation, what equation should we use? You may assume the block is being accelerated up the slope.
Draw the force diagram before you do any calculations.
Unlike the previous example, $T$ is acting opposite to $mg\sin\theta$, so you should use the rule "$F_{same} - F_{opposite} = ma$" to find the magnitude of the acceleration (see
lecture 04a for a reminder).
Solution
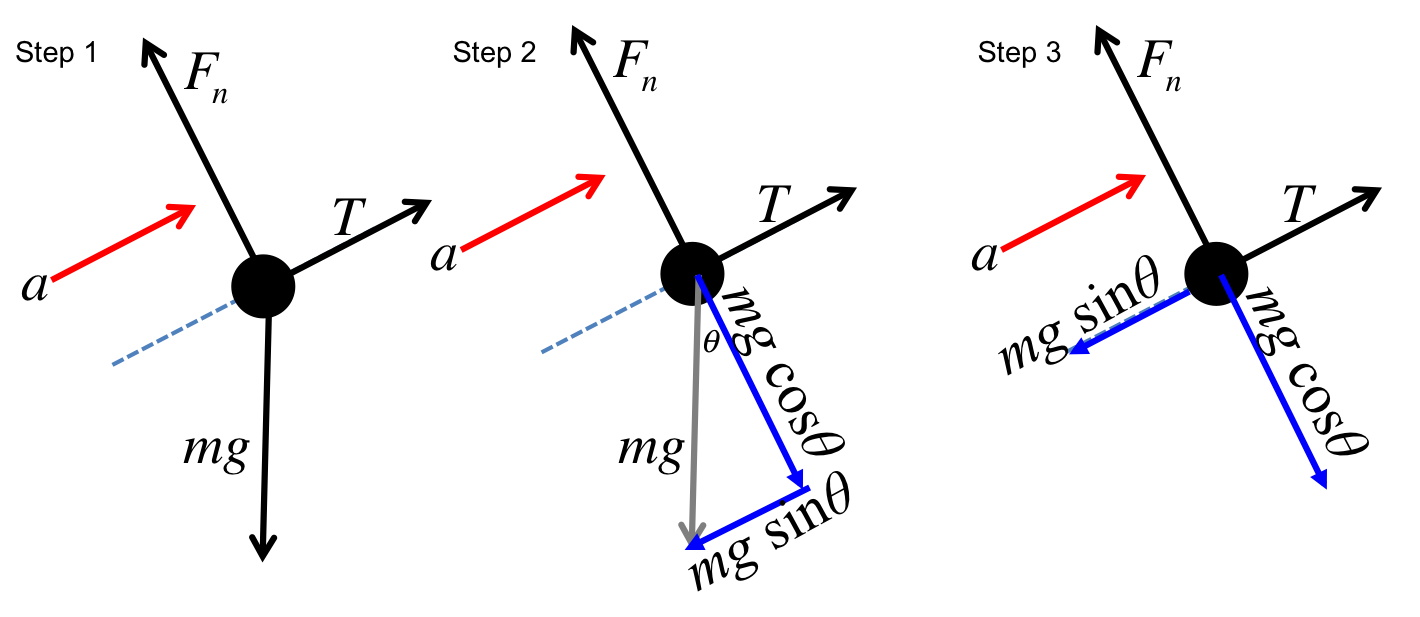
From the force diagram, and the rule "$F_{same} - F_{opposite} = ma$" for opposing forces, we have $mg\sin\theta - T = ma$.
$mg\sin\theta = ma$
Incorrect. You forgot to take $T$ into account.
$mg\sin\theta + T = ma$
Incorrect. $T$ is acting opposite to $mg\sin\theta$ so they should not be added together.
$T - mg\sin\theta = ma$
Correct!
$mg\sin\theta - T = ma$
Incorrect. Note that $T$ is in the same direction as $a$ so should not be preceded by a negative sign.
$mg\cos\theta + T = ma$
Incorrect. $a$ is along the parallel direction, so $mg\cos\theta$ (which points in the perpendicular direction) should not be involved.
$T - mg\cos\theta = ma$
Incorrect. $a$ is along the parallel direction, so $mg\cos\theta$ (which points in the perpendicular direction) should not be involved.
2
Feedback will appear here.
force || incline
Exercise - pulling a block up a frictionless incline 2
Continue from the previous problem. Solve for the magnitude of the acceleration and the normal force.
The normal force can be found the same way as all previous examples of incline. $T$ does not affect its calculation because it is perpendicular to $F_n$.
Solution
Using the equation found in the previous part:
$$
\begin{eqnarray}
T - mg\sin\theta &=& ma \\
\Rightarrow a &=& \frac{T}{m} - g\sin\theta \\
&=& \frac{15}{2} - 9.8\sin 30^\circ \\
&=& 7.5 - 4.9 = 2.6m/s^2
\end{eqnarray}
$$
$T$ does not affect its calculation because it is perpendicular to $F_n$. Since $a_\perp = 0$, we have $F_n = mg\cos30^\circ = 16.97N$.
$a=$
2.6
0.2
$m/s^2$
$F_n=$
16.97
0.2
$N$
Feedback will appear here.
force || multi_body
Example - horizontal force on two blocks
A force \(F=60N\) is applied to two blocks (\(m_1=1kg, m_2=2kg\)). Find the accerleration \(a\) and the tension \(T\) between the blocks.
Solution
Begin by drawing 2 separate free-body diagrams, one for each object:
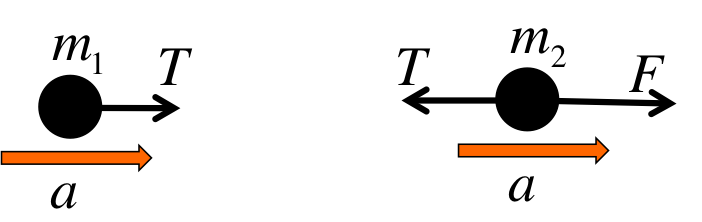 For simplicity we only included the horizontal forces because the motion is clearly purely horizontal. The vertical forces like the normal forces and the weight cancel out.
For simplicity we only included the horizontal forces because the motion is clearly purely horizontal. The vertical forces like the normal forces and the weight cancel out.
Now treat the diagrams as if they are two separate problems and apply the 2nd Law to each:
$$
\begin{eqnarray}
T&=&m_1 a \\
F-T &=& m_2 a
\end{eqnarray}
$$
From these 2 equations, we can solve for the 2 unknowns \(a\) and \(T\). The fastest way to do it is by adding the equations together (usually the action and reaction forces, which are \(T\) and \(-T\) here will cancel out):
$$
\begin{eqnarray}
F &=& m_1 a + m_2 a = (m_1+m_2)a \\
\Rightarrow a &=& \frac{F}{m_1+m_2} \\
&=& \frac{60N}{1kg+2kg} = 20m/s^2
\end{eqnarray}
$$
Substituting \(a=20m/s^2\) back into either one of the equations earlier gives the tension:
$$
\begin{eqnarray}
T&=&m_1 a = (1kg)(20m/s^2) = 20N
\end{eqnarray}
$$
force || multi_body || normal_force
Example - force applied at an angle on two blocks 1
A force \(F=30N\) at angle of \(\theta = 20^\circ\) to the horizontal is applied to two blocks (\(m_1=1kg, m_2=2kg\)). Find the accerleration \(a\) and the tension \(T\) between the blocks.
Solution
We will begin by decomposing the force \(F\):
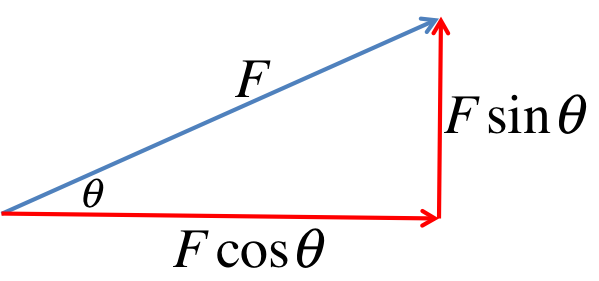 Noting that both \(a\) and \(T\) are horizontal, we draw the free-body diagrams of each object, including only the horizontal forces (we will look at the verticl forces in the follow-up question here):
Noting that both \(a\) and \(T\) are horizontal, we draw the free-body diagrams of each object, including only the horizontal forces (we will look at the verticl forces in the follow-up question here):

One can see that the force diagrams are essentially the same as the previous example, the only difference is that \(F\) is now replaced by \(F\cos\theta\). The calculation of \(a\) and \(T\) therefore proceed exactly as before. The 2nd Law on each of the two force diagrams give:
$$
\begin{eqnarray}
T&=&m_1 a \\
F\cos \theta-T &=& m_2 a
\end{eqnarray}
$$
Adding the equations give:
$$
\begin{eqnarray}
F\cos\theta &=& m_1 a + m_2 a = (m_1+m_2)a \\
\Rightarrow a &=& \frac{F\cos\theta}{m_1+m_2} \\
&=& \frac{30N \cos 20^\circ}{1kg+2kg} = 9.40 m/s^2
\end{eqnarray}
$$
Substituting \(a=20m/s^2\) back into either one of the equations earlier gives the tension:
$$
\begin{eqnarray}
T&=&m_1 a = (1kg)(9.40m/s^2) = 9.40N
\end{eqnarray}
$$
force || multi_body || normal_force
Example - force applied at an angle on two blocks 2
Continue from the previous problem. Calculate the normal forces \(F_{n1}\) and \(F_{n2}\) acting on the two masses.
Solution
Just like before, we begin by drawing the free-body diagrams, one for each object, but this time focus on the vertical forces (because the normal forces are vertical):
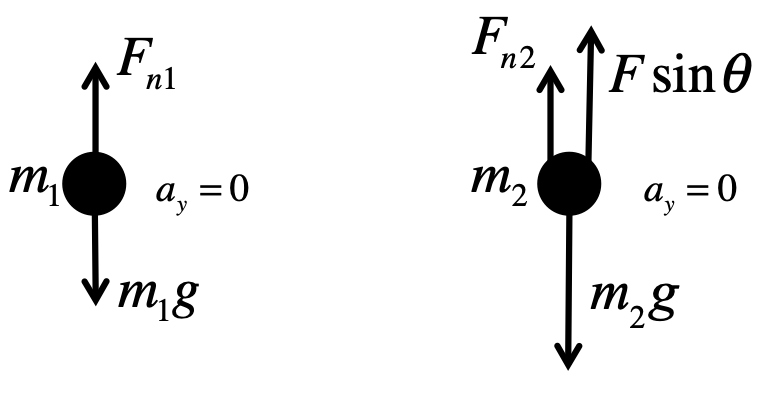 Note that the force \(F\) acting on \(m_2\) has been decomposed as in the last problem, and only the vertical component \(F\sin\theta\) is kept. Because there is no motion vertically, we know the vertical acceleration is zero, i.e. \(a_y = 0\). This implies all the vertical forces must cancel out.
Note that the force \(F\) acting on \(m_2\) has been decomposed as in the last problem, and only the vertical component \(F\sin\theta\) is kept. Because there is no motion vertically, we know the vertical acceleration is zero, i.e. \(a_y = 0\). This implies all the vertical forces must cancel out.
For \(m_1\):
$$
\begin{eqnarray}
F_{n1} &=& m_1 g = (1kg)(9.8m/s^2) = 9.8N
\end{eqnarray}
$$
For \(m_2\):
$$
\begin{eqnarray}
F_{n2} + F\sin\theta &=& m_2 g \\
\Rightarrow F_{n2} &=& m_2 g - F\sin\theta \\
&=& (2)(9.8) - 30\sin 20^\circ \\
&=& 19.6N - 10.26N = 9.34N
\end{eqnarray}
$$
force || pulley || multi-body
Exercise - two blocks and a pulley without friction 1
A block $m_1= 10kg$ is being on a frictionless table with another block $m_2=20kg$. We wish to find the magnitude of the accerlation and the tension. Given the free-body diagrams, what is the equation to use for $m_1$?
$T=m_1 a$
Correct!
$m_2g = m_1 a$
Incorrect. There is only one force $T$ acting on $m_1$ in the force diagram. The gravitational force $m_2 g$ does not act on $m_1$ directly.
$T - m_2g = m_1 a$
Incorrect. There is only one force $T$ acting on $m_1$ in the force diagram. The gravitational force $m_2 g$ does not act on $m_1$ directly.
$m_2g - T = m_1 a$
Incorrect. There is only one force $T$ acting on $m_1$ in the force diagram. The gravitational force $m_2 g$ does not act on $m_1$ directly.
0
Feedback will appear here.
force || pulley || multi-body
Exercise - two blocks and a pulley without friction 2
Continue from the previous problem. What is the equation to use for $m_2$ in order to find the magnitude of the acceleration?
$T=m_2 a$
Incorrect. $T$ is not the only force acting on $m_2$.
$m_2g = m_2 a$
Incorrect. Gravity is not the only force on $m_2$.
$T - m_2g = m_2 a$
Incorrect. In our convention, we always put the forces in the same direction as $a$ first, minus the forces opposite to $a$, i.e. $F_{same} - F_{opposite} = ma$.
$m_2g - T = m_2 a$
Correct.
3
Feedback will appear here.
force || pulley || multi-body
Exercise - two blocks and a pulley without friction 3
Continue from the previous problem. Find the magnitude of the acceleration and the tension.
Add the two equation you obtained from the previous two problems to solve for $a$. Then substitute back to get $T$.
Solution
From the free-body diagrams and the last two problems, we obtain the equations:
$$
\begin{eqnarray}
T &=& m_1 a \\
m_2 g - T &=& m_2 a
\end{eqnarray}
$$
Adding the equations we get:
$$
\begin{eqnarray}
m_2 g &=& m_1 a + m_2 a = (m_1 + m_2) a \\
a &=& \frac{m_2 g}{m_1 + m_2} \\
&=& \frac{(20)(9.8)}{10 + 20} \\
&=& 6.53m/s^2
\end{eqnarray}
$$
Substitute back into $T = m_1 a$ gives $T= (10)(6.53) = 65.3N$.
$a=$
6.53
0.2
$m/s^2$
$T = $
65.3
0.2
$N$
Feedback will appear here.
force || friction || normal_force
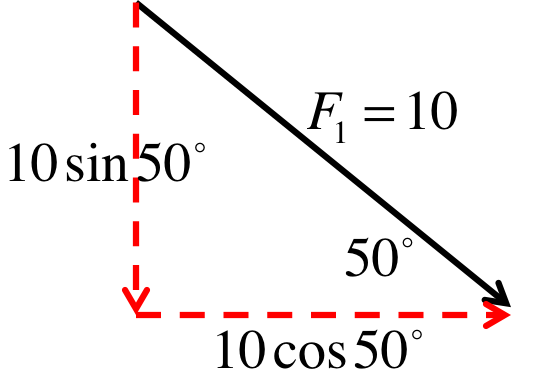
Example - moving a block with friction 1
A block $m=2kg$ is being pushed with a force $F_1=10N$ at $\theta = 50^\circ$ below the horizontal. Given the coefficient of kinetic friction is $0.12$, find the acceleration of the block.
Solution
For any problems involving friction, it is always a good idea to figure out the normal force first (because it is need to find friction). This problem was actually tackled in Chapter 04a, but here is a reminder.
First we decompose the vector $F_1$, then we collect all the vertical forces in a force diagram (ignoring the horizontal forces for now). Since there is no vertical acceleration, the vertical forces must all cancel out and we get:
$$
\begin{eqnarray}
F_n &=& mg + F_1 \sin 50^\circ = (2)(9.8) + 10 \sin 50^\circ \\
&=& 19.60 + 7.66N = 27.26N
\end{eqnarray}
$$
From this we could calculate the kinetic friction:
$$
\begin{eqnarray}
f &=& \mu F_n \\
&=& (0.12)(27.26N) = 3.27N
\end{eqnarray}
$$
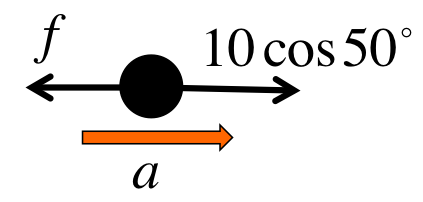
The horizontal forces can now be used to find the acceleration:
$$
\begin{eqnarray}
10\cos 50^\circ - f &=& ma \\
a &=& \frac{10\cos 50^\circ - f}{m} \\
&=& \frac{6.43 - 3.27}{2} = 1.58m/s^2
\end{eqnarray}
$$
=
force || friction || normal_force
Exercise - moving a block with friction 2
A block $m=2kg$ is being pushed with a force $F_2=10N$ at $\theta = 20^\circ$ above the horizontal. Given the coefficient of kinetic friction is $0.12$, we wish to study the acceleration of the block. What is the normal force of the block?
Decompose the force $F_2$ and draw a force diagram for all the vertical forces.
Solution
First we decompose the vector $F_2$, then we collect all the vertical forces in a force diagram (ignoring the horizontal forces for now). Since there is no vertical acceleration, the vertical forces must all cancel out and we get:
$$
\begin{eqnarray}
F_n + 10\sin 20^\circ &=& mg \\
\Rightarrow F_n &=& mg - 10\sin 20^\circ = (2)(9.8) - 10 \sin 20^\circ \\
&=& 19.60 - 3.42N = 16.18N
\end{eqnarray}
$$
$mg + 10\sin 20^\circ$
Incorrect. The upward force $10\sin 20^\circ$ would reduce the normal force, not increase it.
$mg - 10\sin 20^\circ$
Correct!
$10\sin 20^\circ - mg$
Incorrect. Check the sign.
$mg + 10\cos 20^\circ$
Incorrect. $10\cos 20^\circ$ is a horizontal force and should not be involved since $F_n$ is vertical.
1
Feedback will appear here.
force || friction || normal_force
Exercise - moving a block with friction 3
Continue from the previous problem. Find the kinetic friction on the block.
Use $f=\mu F_n$. You have already found $F_n$ in the last problem.
Solution
$$
\begin{eqnarray}
f &=& \mu F_n = (0.12)(16.18N) \\
&=& 1.94 N
\end{eqnarray}
$$
$f=$
1.94
0.1
Select unit:
\(\mu\)
\(m\)
\(N\)
\(m/s^2\)
2
Feedback will appear here.
force || friction || normal_force
Exercise - moving a block with friction 4
Continue from the previous problem. Find the acceleration of the block.
Draw a force diagram of all the horizontal forces ($10\cos 20^\circ$ and $f$) then apply Newton's Second Law.
Solution
There are only two horizontal forces, so the 2nd Law gives:
$$
\begin{eqnarray}
10\cos 20^\circ - f &=& ma \\
a &=& \frac{10\cos 20^\circ - f}{m} \\
&=& \frac{9.40 - 1.94}{2} \\
&=& 3.73m/s^2
\end{eqnarray}
$$
$a=$
3.73
0.2
Select unit:
$m$
$\mu$
$N$
$m/s^2$
3
Feedback will appear here.
force || centripetal || circular_motion
Example - centripetal acceleration and centripetal force (simple)
A ball $m = 5kg$ is tied to a string $0.4m$ long and swung around at $2m/s$. Find the centripetal acceleration and the centripetal force.
Solution
$$
\begin{eqnarray}
a_{cent} &=& \frac{v^2}{r} = \frac{2^2}{0.4} = 10m/s^2 \\
F_{cent} &=& m a = (5)(10) = 50N
\end{eqnarray}
$$
force || centripetal || circular_motion
Example - breaking point
A ball $m = 5kg$ is tied to a string $0.4m$ long and swung around in uniform circular motion. Suppose the string will break if the tension on it exceeds $70N$, find the maximum speed of the ball (without breaking the string).
Solution
$$
\begin{eqnarray}
F_{cent} &=& \frac{mv^2}{r} \leq 70N \\
\Rightarrow v \leq \sqrt{\frac{70 r}{m}} = \sqrt{\frac{70 (0.4)}{5}} \\
\Rightarrow v \leq 2.37m/s
\end{eqnarray}
$$
The maximum speed is $2.37m/s$.
force || centripetal || circular_motion
Exercise - centripetal acceleration and centripetal force (simple)
A ball $m = 5kg$ is tied to a string $0.4m$ long and swung around at $2m/s$. Find the centripetal acceleration and the centripetal force.
Use $a_{cent} = \frac{v^2}{r}$ and $F_{cent} = \frac{mv^2}{r}$.
Solution
$$
\begin{eqnarray}
a_{cent} &=& \frac{v^2}{r} = \frac{2^2}{0.4} = 10m/s^2 \\
F_{cent} &=& m a = (5)(10) = 50N
\end{eqnarray}
$$
$a_{cent}=$
10
0.2
$F_{cent} = $
50
0.2
Select unit:
$m/s^2, m/s^2$
$N, m/s^2$
$m/s^2, N$
$N, N$
2
Feedback will appear here.





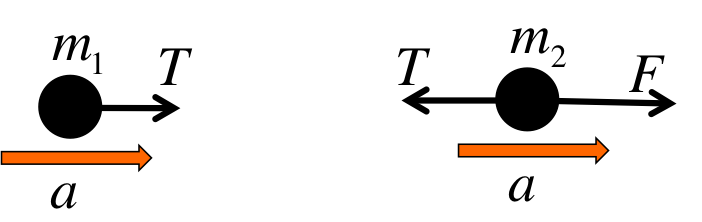 For simplicity we only included the horizontal forces because the motion is clearly purely horizontal. The vertical forces like the normal forces and the weight cancel out.
For simplicity we only included the horizontal forces because the motion is clearly purely horizontal. The vertical forces like the normal forces and the weight cancel out.
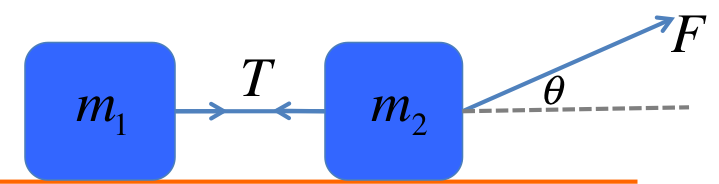
 Noting that both \(a\) and \(T\) are horizontal, we draw the free-body diagrams of each object, including only the horizontal forces (we will look at the verticl forces in the follow-up question
Noting that both \(a\) and \(T\) are horizontal, we draw the free-body diagrams of each object, including only the horizontal forces (we will look at the verticl forces in the follow-up question 
 Note that the force \(F\) acting on \(m_2\) has been decomposed as in the last problem, and only the vertical component \(F\sin\theta\) is kept. Because there is no motion vertically, we know the vertical acceleration is zero, i.e. \(a_y = 0\). This implies all the vertical forces must cancel out.
Note that the force \(F\) acting on \(m_2\) has been decomposed as in the last problem, and only the vertical component \(F\sin\theta\) is kept. Because there is no motion vertically, we know the vertical acceleration is zero, i.e. \(a_y = 0\). This implies all the vertical forces must cancel out.